跳转至

5 地震作用和结构抗震验算

5.1 一般规定

5.1.1

各类建筑结构的地震作用，应符合下列规定：

1 一般情况下，应至少在建筑结构的两个主轴方向分别计算水平地震作用，各方向的水平地震作用应由该方向抗侧力构件承担。

2 有斜交抗侧力构件的结构，当相交角度大于 $ 15^{\circ} $ 时，应分别计算各抗侧力构件方向的水平地震作用。

3 质量和刚度分布明显不对称的结构，应计入双向水平地震作用下的扭转影响；其他情况，应允许采用调整地震作用效应的方法计入扭转影响。

48、9度时的大跨度和长悬臂结构及9度时的高层建筑，应计算竖向地震作用。

注：8、9度时采用隔震设计的建筑结构，应按有关规定计算竖向地震作用。

5.1.2

各类建筑结构的抗震计算，应采用下列方法：

1 高度不超过 40m、以剪切变形为主且质量和刚度沿高度分布比较均匀的结构，以及近似于单质点体系的结构，可采用底部剪力法等简化方法。

2 除 1 款外的建筑结构，宜采用振型分解反应谱法。

3 特别不规则的建筑、甲类建筑和表 5.1.2-1 所列高度范围的高层建筑，应采用时程分析法进行多遇地震下的补充计算；当取三组加速度时程曲线输入时，计算结果宜取时程法的包络值和振型分解反应谱法的较大值；当取七组及七组以上的时程曲线时，计算结果可取时程法的平均值和振型分解反应谱法的较大值。

采用时程分析法时，应按建筑场地类别和设计地震分组选用实际强震记录和人工模拟的加速度时程曲线，其中实际强震记录的数量不应少于总数的2/3，多组时程曲线的平均地震影响系数曲线应与振型分解反应谱法所采用的地震影响系数曲线在统计意义上相符，其加速度时程的最大值可按表5.1.2-2采用。弹性时程分析时，每条时程曲线计算所得结构底部剪力不应小于振型分解反应谱法计算结果的65%，多条时程曲线计算所得结构底部剪力的平均值不应小于振型分解反应谱法计算结果的80%。

表 5.1.2-1 采用时程分析的房屋高度范围
烈度、场地类别房屋高度范围（m）
8度Ⅰ、Ⅱ类场地和7度>100
8度Ⅲ、Ⅳ类场地>80
9度>60
表 5.1.2-2 时程分析所用地震加速度时程的最大值 $ (\mathrm{cm}/\mathrm{s}^{2}) $
地震影响6度7度8度9度
多遇地震1835(55)70(110)140
罕遇地震125220(310)400(510)620

注：括号内数值分别用于设计基本地震加速度为0.15g和0.30g的地区。

4 计算罕遇地震下结构的变形，应按本规范第 5.5 节规定，采用简化的弹塑性分析方法或弹塑性时程分析法。

5 平面投影尺度很大的空间结构，应根据结构形式和支承条件，分别按单点一致、多点、多向单点或多向多点输入进行抗震计算。按多点输入计算时，应考虑地震行波效应和局部场地效应。6度和7度Ⅰ、Ⅱ类场地的支承结构、上部结构和基础的抗震验算可采用简化方法，根据结构跨度、长度不同，其短边构件可乘以附加地震作用效应系数1.15～1.30；7度Ⅲ、Ⅳ类场地和8、9度时，应采用时程分析方法进行抗震验算。

6 建筑结构的隔震和消能减震设计，应采用本规范第 12 章规定的计算方法。

7 地下建筑结构应采用本规范第 14 章规定的计算方法。

5.1.3

计算地震作用时，建筑的重力荷载代表值应取结构和构配件自重标准值和各可变荷载组合值之和。各可变荷载的组合值系数，应按表5.1.3采用。

表 5.1.3 组合值系数
可变荷载种类组合值系数
雪荷载0.5
屋面积灰荷载0.5
屋面活荷载不计入
按实际情况计算的楼面活荷载1.0
按等效均布荷载计算的楼面活荷载藏书库、档案库0.8
其他民用建筑0.5
起重机悬吊物重力硬钩吊车0.3
软钩吊车不计入

注：硬钩吊车的吊重较大时，组合值系数应按实际情况采用。

5.1.4

建筑结构的地震影响系数应根据烈度、场地类别、设计地震分组和结构自振周期以及阻尼比确定。其水平地震影响系数最大值应按表5.1.4-1采用；特征周期应根据场地类别和设计地震分组按表5.1.4-2采用，计算罕遇地震作用时，特征周期应增加0.05s。

注：周期大于 6.0s 的建筑结构所采用的地震影响系数应专门研究。

表 5.1.4-1 水平地震影响系数最大值
地震影响6度7度8度9度
多遇地震0.040.08(0.12)0.16(0.24)0.32
罕遇地震0.280.50(0.72)0.90(1.20)1.40

注：括号中数值分别用于设计基本地震加速度为 0.15g 和 0.30g 的地区。

表 5.1.4-2 特征周期值(s)
设计地震 分组场 地 类 别
I 0I 1IIIIIIV
第一组0.200.250.350.450.65
第二组0.250.300.400.550.75
第三组0.300.350.450.650.90

5.1.5

建筑结构地震影响系数曲线（图 5.1.5）的阻尼调整和形状参数应符合下列要求：

1 除有专门规定外，建筑结构的阻尼比应取 0.05，地震影响系数曲线的阻尼调整系数应按 1.0 采用，形状参数应符合下列规定：

1）直线上升段，周期小于0.1s的区段。

2）水平段，自0.1s至特征周期区段，应取最大值 $ \left(\alpha_{\max}\right) $

3）曲线下降段，自特征周期至5倍特征周期区段，衰减指数应取0.9。

4）直线下降段，自5倍特征周期至6s区段，下降斜率调整系数应取0.02。

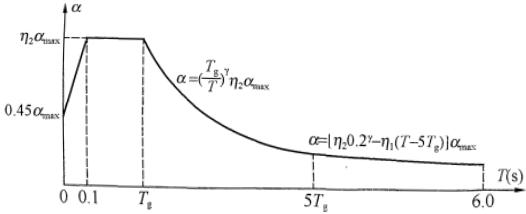
Image
图 5.1.5 地震影响系数曲线

α—地震影响系数； $ \alpha_{max} $ —地震影响系数最大值；

$ \eta_{1} $ 一直线下降段的下降斜率调整系数； $ \gamma $ —衰减指数；

$ T_{8} $ --特征周期； $ \eta_{2} $ —阻尼调整系数；T—结构自振周期

2 当建筑结构的阻尼比按有关规定不等于 0.05 时，地震影响系数曲线的阻尼调整系数和形状参数应符合下列规定：

1）曲线下降段的衰减指数应按下式确定：

$$ \gamma=0.9+\frac{0.05-\zeta}{0.3+6\zeta} \tag{5.1.5-1} $$

式中： $ \gamma $ ——曲线下降段的衰减指数；

$ \zeta $ ——阻尼比。

2）直线下降段的下降斜率调整系数应按下式确定：

$$ \eta_{1}=0.02+\frac{0.05-\zeta}{4+32\zeta} \tag{5.1.5-2} $$

式中： $ \eta_{1} $ ——直线下降段的下降斜率调整系数，小于0时取0。

3）阻尼调整系数应按下式确定：

$$ \eta_{2}=1+\frac{0.05-\zeta}{0.08+1.6\zeta} \tag{5.1.5-3} $$

式中： $ \eta_{2} $ ——阻尼调整系数，当小于0.55时，应取0.55。

5.1.6

结构的截面抗震验算，应符合下列规定：

16度时的建筑（不规则建筑及建造于Ⅳ类场地上较高的高层建筑除外），以及生土房屋和木结构房屋等，应符合有关的抗震措施要求，但应允许不进行截面抗震验算。

2 6度时不规则建筑、建造于Ⅳ类场地上较高的高层建筑，7度和7度以上的建筑结构（生土房屋和木结构房屋等除外），应进行多遇地震作用下的截面抗震验算。

注：采用隔震设计的建筑结构，其抗震验算应符合有关规定。

5.1.7

符合本规范第 5.5 节规定的结构，除按规定进行多遇地震作用下的截面抗震验算外，尚应进行相应的变形验算。

5.2 水平地震作用计算

5.2.1

采用底部剪力法时，各楼层可仅取一个自由度，结构的水平地震作用标准值，应按下列公式确定

(图 5.2.1):

$$ F_{\mathrm{Ek}}=\alpha_{1}G_{\mathrm{eq}} \tag{5.2.1-1} $$

$$ F_{i}=\frac{G_{i}H_{i}}{\sum_{j=1}^{n}G_{j}H_{j}}F_{\mathrm{E k}}(1-\delta_{n})(i=1,2,\cdots n) \tag{5.2.1-2} $$

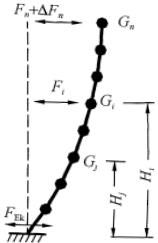
Image

$$ \Delta F_{n}=\delta_{n}F_{\mathrm{E k}} \tag{5.2.1-3} $$

式中： $ F_{Ek} $ ——结构总水平地震作用标准值；

图 5.2.1 结构水平地震作用计算简图

$ \alpha_{1} $ ——相应于结构基本自振周期的

水平地震影响系数值，应按本规范第5.1.4、第5.1.5条确定，多层砌体房屋、底部框架砌体房屋，宜取水平地震影响系数最大值；

$ G_{eq} $ ——结构等效总重力荷载，单质点应取总重力荷载代表值，多质点可取总重力荷载代表值的85%；

$ F_{i} $ ——质点 i 的水平地震作用标准值；

$ G_{i} $ 、 $ G_{j} $ ——分别为集中于质点 i、j 的重力荷载代表值，应按本规范第 5.1.3 条确定；

$ \bar{H}{i} $ 、 $ H $ ——分别为质点 i、j 的计算高度；

$ \delta_{n} $ ——顶部附加地震作用系数，多层钢筋混凝土和钢结构房屋可按表5.2.1采用，其他房屋可采用0.0；

$ \Delta F_{n} $ ——顶部附加水平地震作用。

表 5.2.1 顶部附加地震作用系数
$ T_{g}(s) $$ T_{1}>1.4T_{g} $$ T_{1}\leq1.4T_{g} $
$ T_{g}\leq0.35 $$ 0.08T_{1}+0.07 $0.0
$ 0.35<T_{g}\leq0.55 $$ 0.08T_{1}+0.01 $
$ T_{g}>0.55 $$ 0.08T_{1}-0.02 $

注： $ T_{1} $ 为结构基本自振周期。

5.2.2

采用振型分解反应谱法时，不进行扭转耦联计算的结构，应按下列规定计算其地震作用和作用效应：

1 结构 j 振型 i 质点的水平地震作用标准值，应按下列公式确定：

$$ F_{ji}=\alpha_{j}\gamma_{j}X_{ji}G_{i}\quad(i=1,2,\cdots n,j=1,2,\cdots m) \tag{5.2.2-1} $$

$$ \gamma_{j}=\sum_{i=1}^{n}X_{ji}G_{i}/\sum_{i=1}^{n}X_{ji}^{2}G_{i} \tag{5.2.2-2} $$

式中： $ F_{ji} $ —— j 振型 i 质点的水平地震作用标准值；

$ \alpha_{j} $ ——相应于 j 振型自振周期的地震影响系数，应按本规范第 5.1.4、第 5.1.5 条确定；

$ X_{ji} $ ——j振型i质点的水平相对位移；

$ \gamma_{i} $ —— j 振型的参与系数。

2 水平地震作用效应（弯矩、剪力、轴向力和变形），当相邻振型的周期比小于0.85时，可按下式确定：

$$ S_{\mathrm{Ek}}=\sqrt{\sum\ S_{j}^{2}} \tag{5.2.2-3} $$

式中： $ S_{Ek} $ ——水平地震作用标准值的效应；

$ S_{j} $ ——j 振型水平地震作用标准值的效应，可只取前 2～3 个振型，当基本自振周期大于 1.5s 或房屋高宽比大于 5 时，振型个数应适当增加。

5.2.3

水平地震作用下，建筑结构的扭转耦联地震效应应符合下列要求：

1 规则结构不进行扭转耦联计算时，平行于地震作用方向的两个边榀各构件，其地震作用效应应乘以增大系数。一般情况下，短边可按 1.15 采用，长边可按 1.05 采用；当扭转刚度较小时，周边各构件宜按不小于 1.3 采用。角部构件宜同时乘以两个方向各自的增大系数。

2 按扭转耦联振型分解法计算时，各楼层可取两个正交的水平位移和一个转角共三个自由度，并应按下列公式计算结构的地震作用和作用效应。确有依据时，尚可采用简化计算方法确定地震作用效应。

1）j 振型 i 层的水平地震作用标准值，应按下列公式确定：

$$ \begin{array}{r}{F_{x j i}=\alpha_{j}\gamma_{v j}X_{j i}G_{i}}\ {F_{y j i}=\alpha_{j}\gamma_{v j}Y_{j i}G_{i}\quad(i=1,2,\cdots n,j=1,2,\cdots m)}\ {F_{v j i}=\alpha_{j}\gamma_{v j}r_{i}^{2}\varphi_{j i}G_{i}}\end{array} \tag{5.2.3-1} $$

式中： $ F_{xji} $ 、 $ F_{yji} $ 、 $ F_{vji} $ ——分别为j振型i层的x方向、y方向和转角方向的地震作用标准值；

$ X_{ji} $ 、 $ Y_{ji} $ ——分别为j振型i层质心在x、y方向的水平相对位移；

$ \varphi_{ji} $ ——j 振型 i 层的相对扭转角；

$ r_{i} $ ——i层转动半径，可取i层绕质心的转动惯量除以该层质量的商的正二次方根；

$ \gamma_{ij} $ ——计入扭转的 j 振型的参与系数，可按下列公式确定：

当仅取 x 方向地震作用时

$$ \gamma_{t j}=\sum_{i=1}^{n}X_{j i}G_{i}/\sum_{i=1}^{n}(X_{j i}^{2}+Y_{j i}^{2}+\varphi_{j i}^{2}r_{i}^{2})G_{i} \tag{5.2.3-2} $$

当仅取 y 方向地震作用时

$$ \gamma_{\mathrm{v}}=\sum_{i=1}^{n}Y_{j i}G_{i}/\sum_{i=1}^{n}(X_{j i}^{2}+Y_{j i}^{2}+\varphi_{j i}^{2}r_{i}^{2})G_{i} \tag{5.2.3-3} $$

当取与 x 方向斜交的地震作用时，

$$ \gamma_{v j}=\gamma_{x j}\mathrm{c o s}\theta+\gamma_{y j}\mathrm{s i n}\theta \tag{5.2.3-4} $$

式中： $ \gamma_{xj} $ 、 $ \gamma_{yj} $ ——分别由式（5.2.3-2）、式（5.2.3-3）求得的参与系数；

$ \theta $ ——地震作用方向与 x 方向的夹角。

2）单向水平地震作用下的扭转耦联效应，可按下列公式确定：

$$ S_{Ek}=\sqrt{\sum_{j=1}^{m}\sum_{k=1}^{m}\rho_{jk}S_{j}S_{k}} \tag{5.2.3-5} $$

$$ \rho_{jk}=\frac{8\sqrt{\zeta_{j}\zeta_{k}}(\zeta_{j}+\lambda_{T}\zeta_{k})\lambda_{T}^{1.5}}{(1-\lambda_{T}^{2})^{2}+4\zeta_{j}\zeta_{k}(1+\lambda_{T}^{2})\lambda_{T}+4(\zeta_{j}^{2}+\zeta_{k}^{2})\lambda_{T}^{2}} \tag{5.2.3-6} $$

式中： $ S_{Ek} $ ——地震作用标准值的扭转效应；

$ S_{j} $ 、 $ S_{k} $ ——分别为j、k振型地震作用标准值的效应，可取前9～15个振型；

$ \zeta_{j} $ 、 $ \zeta_{k} $ ——分别为j、k振型的阻尼比；

$ \rho_{jk} $ ——j 振型与 k 振型的耦联系数；

$ \lambda_{T} $ ——k 振型与 j 振型的自振周期比。

3）双向水平地震作用下的扭转耦联效应，可按下列公式中的较大值确定：

$$ S_{\mathrm{Ek}}=\sqrt{S_{\mathrm{x}}^{2}+(0.85S_{\mathrm{y}})^{2}} \tag{5.2.3-7} $$

或

$$ S_{\mathrm{Ek}}=\sqrt{S_{\mathrm{y}}^{2}+(0.85S_{\mathrm{x}})^{2}} \tag{5.2.3-8} $$

式中， $ S_{x} $ 、 $ S_{y} $ 分别为 x 向、y 向单向水平地震作用按式（5.2.3-5）计算的扭转效应。

5.2.4

采用底部剪力法时，突出屋面的屋顶间、女儿墙、烟囱等的地震作用效应，宜乘以增大系数3，此增大部分不应往下传递，但与该突出部分相连的构件应予计入；采用振型分解法时，突出屋面部分可作为一个质点；单层厂房突出屋面天窗架的地震作用效应的增大系数，应按本规范第9章的有关规定采用。

5.2.5

抗震验算时，结构任一楼层的水平地震剪力应符合下式要求：

$$ \mathbf{V}{\mathbf{E}\mathbf{K}i}>\lambda\sum $$}^{n}\mathbf{G}_{j} \tag{5.2.5-1

式中： $ V_{EKi} $ ——第 i 层对应于水平地震作用标准值的楼层剪力；

$ \lambda $ ——剪力系数，不应小于表 5.2.5 规定的楼层最小地震剪力系数值，对竖向不规则结构的薄弱层，尚应乘以 1.15 的增大系数；

$ G_{j} $ ——第 j 层的重力荷载代表值。

表 5.2.5 楼层最小地震剪力系数值
类别6度7度8度9度
扭转效应明显或基本周期小于3.5s的结构0.0080.016(0.024)0.032(0.048)0.064
基本周期大于5.0s的结构0.0060.012(0.018)0.024(0.036)0.048

注：1 基本周期介于3.5s和5s之间的结构，按插入法取值；

2 括号内数值分别用于设计基本地震加速度为 0.15g 和 0.30g 的地区。

5.2.6

结构的楼层水平地震剪力，应按下列原则分配：

1 现浇和装配整体式混凝土楼、屋盖等刚性楼、屋盖建筑，宜按抗侧力构件等效刚度的比例分配。

2 木楼盖、木屋盖等柔性楼、屋盖建筑，宜按抗侧力构件

从属面积上重力荷载代表值的比例分配。

3 普通的预制装配式混凝土楼、屋盖等半刚性楼、屋盖的建筑，可取上述两种分配结果的平均值。

4 计入空间作用、楼盖变形、墙体弹塑性变形和扭转的影响时，可按本规范各有关规定对上述分配结果作适当调整。

5.2.7

结构抗震计算，一般情况下可不计入地基与结构相互作用的影响；8度和9度时建造于Ⅲ、Ⅳ类场地，采用箱基、刚性较好的筏基和桩箱联合基础的钢筋混凝土高层建筑，当结构基本自振周期处于特征周期的1.2倍至5倍范围时，若计入地基与结构动力相互作用的影响，对刚性地基假定计算的水平地震剪力可按下列规定折减，其层间变形可按折减后的楼层剪力计算。

1 高宽比小于 3 的结构，各楼层水平地震剪力的折减系数，可按下式计算：

$$ \psi=\left(\frac{T_{1}}{T_{1}+\Delta T}\right)^{0.9} \tag{5.2.7-1} $$

式中： $ \psi $ ——计入地基与结构动力相互作用后的地震剪力折减系数；

$ T_{1} $ ——按刚性地基假定确定的结构基本自振周期（s）；

$ \Delta T $ ——计入地基与结构动力相互作用的附加周期（s），可按表5.2.7采用。

表 5.2.7 附加周期（s）
烈 度场 地 类 别
Ⅲ类Ⅳ类
80.080.20
90.100.25

2 高宽比不小于 3 的结构，底部的地震剪力按第 1 款规定折减，顶部不折减，中间各层按线性插入值折减。

3 折减后各楼层的水平地震剪力，应符合本规范第 5.2.5 条的规定。

5.3 竖向地震作用计算

5.3.1

9度时的高层建筑，其竖向地震作用标准值应按下列公式确定（图5.3.1）；楼层的竖向地震作用效应

可按各构件承受的重力荷载代表值的比例分配，并宜乘以增大系数1.5。

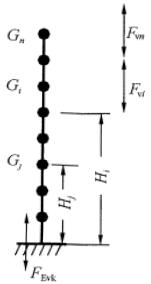
$$ F_{\mathrm{Evk}}=\alpha_{\mathrm{vmax}}G_{\mathrm{eq}} \tag{5.3.1-1} $$

$$ F_{\mathrm{v}i}=\frac{G_{i}H_{i}}{\sum G_{j}H_{j}}F_{\mathrm{Evk}} \tag{5.3.1-2} $$

式中： $ F_{Evk} $ ——结构总竖向地震作用标准值；

Image

$ F_{vi} $ ——质点 i 的竖向地震作用标准值；

$ \alpha_{vmax} $ ——竖向地震影响系数的最大值，可取水平地震影响系数最大值的65%；

图 5.3.1 结构竖向地震作用计算简图

$ G_{eq} $ ——结构等效总重力荷载，可取其重力荷载代表值的75%。

5.3.2

跨度、长度小于本规范第5.1.2条第5款规定且规则的平板型网架屋盖和跨度大于24m的屋架、屋盖横梁及托架的竖向地震作用标准值，宜取其重力荷载代表值和竖向地震作用系数的乘积；竖向地震作用系数可按表5.3.2采用。

表 5.3.2 竖向地震作用系数
结构类型烈度场地类别
ⅠⅡⅢ、Ⅳ
平板型网架、 钢屋架8可不计算(0.10)0.08(0.12)0.10(0.15)
90.150.150.20
钢筋混凝土屋架80.10(0.15)0.13(0.19)0.13(0.19)
90.200.250.25

注：括号中数值用于设计基本地震加速度为0.30g的地区。

5.3.3

长悬臂构件和不属于本规范第 5.3.2 条的大跨结构的竖

向地震作用标准值，8度和9度可分别取该结构、构件重力荷载代表值的10%和20%，设计基本地震加速度为0.30g时，可取该结构、构件重力荷载代表值的15%。

5.3.4

大跨度空间结构的竖向地震作用，尚可按竖向振型分解反应谱方法计算。其竖向地震影响系数可采用本规范第5.1.4、第5.1.5条规定的水平地震影响系数的65%，但特征周期可均按设计第一组采用。

5.4 截面抗震验算

5.4.1

结构构件的地震作用效应和其他荷载效应的基本组合，应按下式计算：

$$ S{=}\gamma_{\mathrm{G}}S_{\mathrm{G E}}{+}\gamma_{\mathrm{E h}}S_{\mathrm{E h k}}{+}\gamma_{\mathrm{E v}}S_{\mathrm{E v k}}{+}\psi_{\mathrm{w}}\gamma_{\mathrm{w}}S_{\mathrm{w k}} \tag{5.4.1-1} $$

式中：S——结构构件内力组合的设计值，包括组合的弯矩、轴向力和剪力设计值等；

$ \gamma_{G} $ ——重力荷载分项系数，一般情况应采用1.2，当重力荷载效应对构件承载能力有利时，不应大于1.0；

$ \gamma_{Eh} $ 、 $ \gamma_{Ev} $ ——分别为水平、竖向地震作用分项系数，应按表5.4.1采用；

$ \gamma_{w} $ ——风荷载分项系数，应采用1.4；

$ S_{GE} $ ——重力荷载代表值的效应，可按本规范第5.1.3条采用，但有吊车时，尚应包括悬吊物重力标准值的效应；

$ S_{Ehk} $ ——水平地震作用标准值的效应，尚应乘以相应的增大系数或调整系数；

$ S_{Evk} $ ——竖向地震作用标准值的效应，尚应乘以相应的增大系数或调整系数；

$ S_{wk} $ ——风荷载标准值的效应；

$ \psi_{w} $ ——风荷载组合值系数，一般结构取0.0，风荷载起控制作用的建筑应采用0.2。

注：本规范一般略去表示水平方向的下标。

表 5.4.1 地震作用分项系数
地震作用$ \gamma_{Eh} $$ \gamma_{Ev} $
仅计算水平地震作用1.30.0
仅计算竖向地震作用0.01.3
同时计算水平与竖向地震作用（水平地震为主）1.30.5
同时计算水平与竖向地震作用（竖向地震为主）0.51.3

5.4.2

结构构件的截面抗震验算，应采用下列设计表达式：

$$ S\leqslant R/\gamma_{RE} \tag{5.4.2-1} $$

式中： $ \gamma_{RE} $ ——承载力抗震调整系数，除另有规定外，应按表5.4.2采用；

R——结构构件承载力设计值。

表 5.4.2 承载力抗震调整系数
材料结构构件受力状态$ \gamma_{RE} $
钢柱，梁，支撑，节点板件，螺栓，焊缝柱，支撑强度稳定0.750.80
砌体两端均有构造柱、芯柱的抗震墙其他抗震墙受剪受剪0.91.0
混凝土梁轴压比小于0.15的柱轴压比不小于0.15的柱抗震墙各类构件受弯偏压偏压偏压受剪、偏拉0.750.750.800.850.85

5.4.3

当仅计算竖向地震作用时，各类结构构件承载力抗震调整系数均应采用1.0。

5.5 抗震变形验算

5.5.1

表 5.5.1 所列各类结构应进行多遇地震作用下的抗震变形验算，其楼层内最大的弹性层间位移应符合下式要求：

$$ \Delta u_{\mathrm{e}}\leqslant[\theta_{\mathrm{e}}]h \tag{5.5.1-1} $$

式中： $ \Delta u_{e} $ ——多遇地震作用标准值产生的楼层内最大的弹性层间位移；计算时，除以弯曲变形为主的高层建筑外，可不扣除结构整体弯曲变形；应计入扭转变形，各作用分项系数均应采用1.0；钢筋混凝土结构构件的截面刚度可采用弹性刚度；

$ \left[\theta_{e}\right] $ ——弹性层间位移角限值，宜按表5.5.1采用；

h——计算楼层层高。

表 5.5.1 弹性层间位移角限值
结构类型$ [\theta_{e}] $
钢筋混凝土框架1/550
钢筋混凝土框架-抗震墙、板柱-抗震墙、框架-核心筒1/800
钢筋混凝土抗震墙、筒中筒1/1000
钢筋混凝土框架1/1000
多、高层钢结构1/250

5.5.2

结构在罕遇地震作用下薄弱层的弹塑性变形验算，应符合下列要求：

1 下列结构应进行弹塑性变形验算：

1）8度Ⅲ、Ⅳ类场地和9度时，高大的单层钢筋混凝土柱厂房的横向排架；

2）7～9度时楼层屈服强度系数小于0.5的钢筋混凝土框架结构和框排架结构；

3）高度大于150m的结构；

4）甲类建筑和9度时乙类建筑中的钢筋混凝土结构和钢结构；

5）采用隔震和消能减震设计的结构。

2 下列结构宜进行弹塑性变形验算：

1) 本规范表 5.1.2-1 所列高度范围且属于本规范表 3.4.3-2 所列竖向不规则类型的高层建筑结构；

2）7度Ⅲ、Ⅳ类场地和8度时乙类建筑中的钢筋混凝土结构和钢结构；

3）板柱-抗震墙结构和底部框架砌体房屋；

4）高度不大于150m的其他高层钢结构；

5）不规则的地下建筑结构及地下空间综合体。

楼层屈服强度系数为按钢筋混凝土构件实际配筋和材料强度标准值计算的楼层受剪承载力和按罕遇地震作用标准值计算的楼层弹性地震剪力的比值；对排架柱，指按实际配筋面积、材料强度标准值和轴向力计算的正截面受弯承载力与按罕遇地震作用标准值计算的弹性地震弯矩的比值。

5.5.3

结构在罕遇地震作用下薄弱层（部位）弹塑性变形计算，可采用下列方法：

1 不超过 12 层且层刚度无突变的钢筋混凝土框架和框排架结构、单层钢筋混凝土柱厂房可采用本规范第 5.5.4 条的简化计算法；

2 除 1 款以外的建筑结构，可采用静力弹塑性分析方法或弹塑性时程分析法等。

3 规则结构可采用弯剪层模型或平面杆系模型，属于本规范第3.4节规定的不规则结构应采用空间结构模型。

5.5.4

结构薄弱层（部位）弹塑性层间位移的简化计算，宜符合下列要求：

1 结构薄弱层（部位）的位置可按下列情况确定：

1）楼层屈服强度系数沿高度分布均匀的结构，可取底层；

2）楼层屈服强度系数沿高度分布不均匀的结构，可取该系数最小的楼层（部位）和相对较小的楼层，一般不超过2~3处；

3）单层厂房，可取上柱。

2 弹塑性层间位移可按下列公式计算：

$$ \Delta u_{\mathrm{p}}=\eta_{\mathrm{p}}\Delta u_{\mathrm{e}} \tag{5.5.4-1} $$

或

$$ \Delta u_{\mathrm{p}}=\mu\Delta u_{\mathrm{y}}=\frac{\eta_{\mathrm{p}}}{\xi_{\mathrm{y}}}\Delta u_{\mathrm{y}} \tag{5.5.4-2} $$

式中： $ \Delta u_{p} $ ——弹塑性层间位移；

$ \Delta u_{y} $ ——层间屈服位移；

$ \mu $ ——楼层延性系数；

$ \Delta u_{e} $ ——罕遇地震作用下按弹性分析的层间位移；

$ \eta_{p} $ ——弹塑性层间位移增大系数，当薄弱层（部位）的屈服强度系数不小于相邻层（部位）该系数平均值的0.8时，可按表5.5.4采用。当不大于该平均值的0.5时，可按表内相应数值的1.5倍采用；其他情况可采用内插法取值；

$ \xi_{y} $ ——楼层屈服强度系数。

表 5.5.4 弹塑性层间位移增大系数
结构类型总层数n 或部位ξy
0.50.40.3
多层均匀框架结构2~41.301.401.60
5~71.501.651.80
8~121.802.002.20
单层厂房上柱1.301.602.00

5.5.5

结构薄弱层（部位）弹塑性层间位移应符合下式要求：

$$ \Delta u_{\mathrm{p}}\leqslant[\theta_{\mathrm{p}}]h \tag{5.5.5-1} $$

式中： $ \left[\theta_{p}\right] $ ——弹塑性层间位移角限值，可按表5.5.5采用；对钢筋混凝土框架结构，当轴压比小于0.40时，可提高10%；当柱子全高的箍筋构造比本规范第6.3.9条规定的体积配箍率大30%时，可提高20%，但累计不超过25%；

h——薄弱层楼层高度或单层厂房上柱高度。

表 5.5.5 弹塑性层间位移角限值
结构类型$ [\theta_{p}] $
单层钢筋混凝土柱排架1/30
钢筋混凝土框架1/50
底部框架砌体房屋中的框架-抗震墙1/100
钢筋混凝土框架-抗震墙、板柱-抗震墙、框架-核心筒1/100
钢筋混凝土抗震墙、筒中筒1/120
多、高层钢结构1/50