附录G 桁架节点板在斜腹杆压力作用下的稳定计算
附录 G 桁架节点板在斜腹杆压力作用下的稳定计算
G.0.1 桁架节点板在斜腹杆压力作用下的稳定计算宜采用下列基本假定：
1 图 G0.1 中 B-A-C-D 为节点板失稳时的屈折线，其中 $ \overline{BA} $ 平行于弦杆， $ \overline{CD} \perp \overline{BA} $ 。
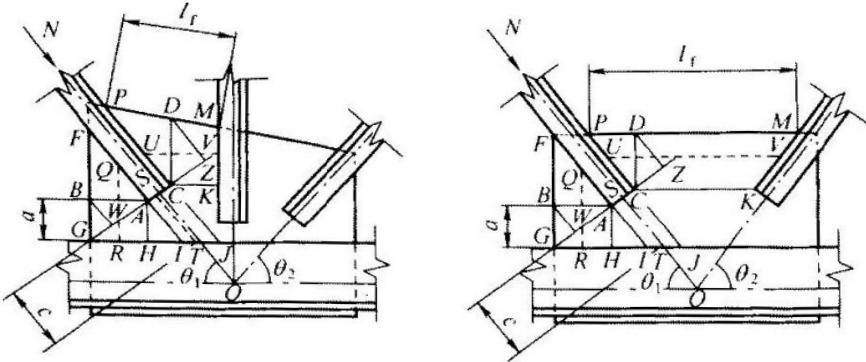
2 在斜腹杆轴向压力 N 的作用下， $ \overline{BA} $ 区（FBGHA 板件）、 $ \overline{AC} $ 区（AIJC 板件）和 $ \overline{CD} $ 区（CKMP 板件）同时受压，当其中某一区先失稳后，其他区即相继失稳。
G.0.2 桁架节点板在斜腹杆压力作用下宜采用下列公式分别计算各区的稳定：
$ \overline{BA} $ 区：
$$ \frac{b_{1}}{(b_{1}+b_{2}+b_{3})}N\sin\theta_{1}\leqslant l_{1}t\varphi_{1}f $$
$ \overline{AC} $ 区：
$$ \frac{b_{2}}{(b_{1}+b_{2}+b_{3})}N\leqslant l_{2}t\varphi_{2}f $$
$$ \overline{CD} 区： $$
$$ \frac{b_{3}}{(b_{1}+b_{2}+b_{3})}N\cos\theta_{1}\leqslant l_{3}t\varphi_{3}f $$
式中：t ——节点板厚度（mm）；
N ——受压斜腹杆的轴向力（N）；
$ l_{1} $ 、 $ l_{2} $ 、 $ l_{3} $ ——分别为屈折线 $ \overline{BA} $ 、 $ \overline{AC} $ 、 $ \overline{CD} $ 的长度（mm）；
$ \varphi_{1} $ 、 $ \varphi_{2} $ 、 $ \varphi_{3} $ ——各受压区板件的轴心受压稳定系数，可按 b 类截面查取；其相应的长细比分别为： $ \lambda_{1}=2.77\frac{\overline{QR}}{t},\lambda_{2}=2.77\frac{\overline{ST}}{t},\lambda_{3}=2.77\frac{\overline{UV}}{t} $ ；式中 $ \overline{QR} $ 、 $ \overline{ST} $ 、 $ \overline{UV} $ 为 $ \overline{BA} $ 、 $ \overline{AC} $ 、 $ \overline{CD} $ 三区受压板件的中线长度；其中 $ \overline{ST}=C;\quad b_{1}\quad(\overline{WA}) $ 、 $ b_{2}\quad(\overline{AC}) $ 、 $ b_{3}\quad(\overline{CZ}) $ 为各屈折线段在有效长度线上的投影长度。
G.0.3 对 $ l_{f}/t > 60\varepsilon_{k} $ 且沿自由边加劲的无竖腹杆节点板（ $ l_{f} $ 为节点板自由边的长度），亦可按本标准第 G.0.2 条计算，只是仅需验算 $ \overline{BA} $ 区和 $ \overline{AC} $ 区，而不必验算 $ \overline{CD} $ 区。