13 钢管连接节点
13 钢管连接节点
13.1 一般规定
13.1.1 本章规定适用于不直接承受动力荷载的钢管桁架、拱架、塔架等结构中的钢管间连接节点。
13.1.2 圆钢管的外径与壁厚之比不应超过 $ 100\varepsilon_{k}^{2} $ ；方（矩）形管的最大外缘尺寸与壁厚之比不应超过 $ 40\varepsilon_{k} $ ， $ \varepsilon_{k} $ 为钢号修正系数。
13.1.3 采用无加劲直接焊接节点的钢管材料应符合本标准第 4.3.7 条的规定。
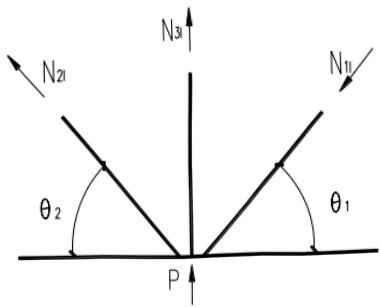
13.1.4 采用无加劲直接焊接节点的钢管桁架，当节点偏心不超过本标准式（13.2.1）限制时，在计算节点和受拉主管承载力时，可忽略因偏心引起的弯矩的影响，但受压主管应考虑按下式计算的偏心弯矩影响。
$$ M=\Delta N\cdot e $$
式中： $ \Delta N $ ——为节点两侧主管轴力之差值；
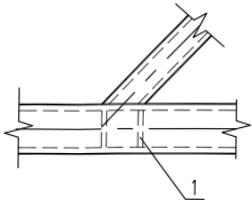
e——为偏心矩（图 13.1.4）。
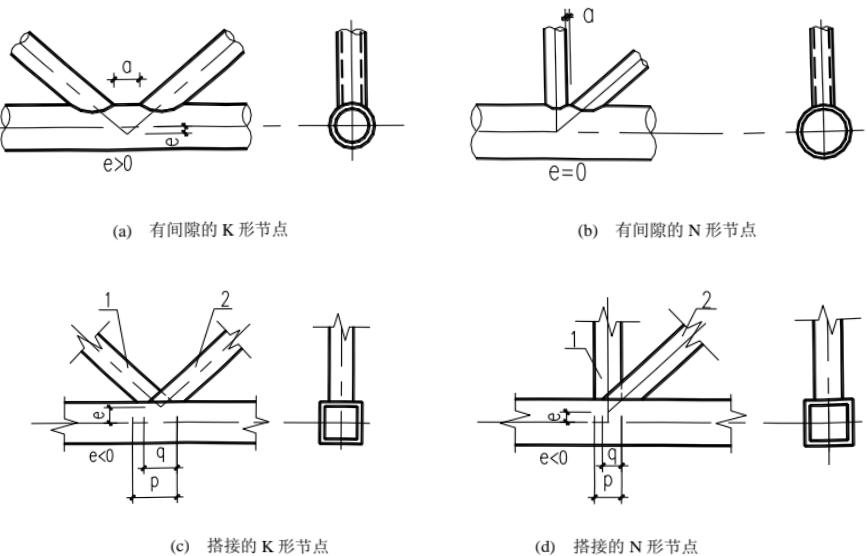
1—搭接管；2—被搭接管
13.1.5 无斜腹杆的空腹桁架采用无加劲钢管直接焊接节点时，应符合本标准附录 H 的规定。
13.2 构造要求
13.2.1 钢管直接焊接节点的构造应符合下列规定：
1 主管的外部尺寸不应小于支管的外部尺寸，主管的壁厚不应小于支管的壁厚，在支管与主管的连接处不得将支管插入主管内。
2 主管与支管或支管轴线间的夹角不宜小于30°。
3 支管与主管的连接节点处宜避免偏心；偏心不可避免时，其值不宜超过下式的限制；
$$ -0.55\leq e/D\left( 或 e/h\right)\leq0.25 $$
式中：e——偏心距（图3.1.4）；
D——圆管主管外径（mm）；
h——连接平面内的方（矩）形管主管截面高度(mm)。
4 支管端部应使用自动切管机切割，支管壁厚小于 $ 6 ~mm $ 时可不切坡口。
5 支管与主管的连接焊缝，除支管搭接应符合本标准第 13.2.2 条的规定外，应沿全周连续焊接并平滑过渡；焊缝形式可沿全周采用角焊缝，或部分采用对接焊缝，部分采用角焊缝，其中支管管壁与主管管壁之间的夹角大于或等于 $ 120^{\circ} $ 的区域宜采用对接焊缝或带坡口的角焊缝，角焊缝的焊脚尺寸不宜大于支管壁厚的 2 倍；搭接支管周边焊缝宜为 2 倍支管壁厚。
6 在主管表面焊接的相邻支管的间隙 a 不应小于两支管壁厚之和（图 13.1.4（a）、（b））。
13.2.2 支管搭接型的直接焊接节点的构造尚应符合下列规定：
1 支管搭接的平面 K 形或 N 形节点（图 13.2.2（a）、（b）），其搭接率 $ \eta_{ov} = q / p \times 100\% $ 应满足 $ 25\% \leq \eta_{ov} \leq 100\% $ ，且应确保在搭接的支管之间的连接焊缝能可靠地传递内力；
2 当互相搭接的支管外部尺寸不同时，外部尺寸较小者应搭接在尺寸较大者上；当支管壁厚不同时，较小壁厚者应搭接在较大壁厚者上；承受轴心压力的支管宜在下方。
1—搭接支管；2—被搭接支管
13.2.3 无加劲直接焊接方式不能满足承载力要求时，可按下列规定在主管内设置横向加劲板：
1 支管以承受轴力为主时，可在主管内设1道或2道加劲板（图13.2.3-1（a），图13.2.3-1（b））；节点需满足抗弯连接要求时，应设2道加劲板；加劲板中面宜垂直主管轴线；当主管为圆管，设置1道加劲板时，加劲板宜设置在支管与主管相贯面的鞍点处，设置2道加劲板时，加劲板宜设置在距相贯面冠点 $ 0.1D_{1} $ 附近（图13.2.3-1（b））， $ D_{1} $ 为支管外径；主管为方管时，加劲肋宜设置2块（图13.2.3-2）。
2 加劲板厚度不得小于支管壁厚，也不宜小于主管壁厚的 2/3 和主管内径的 1/40；加劲板中央开孔时，环板宽度与板厚的比值不宜大于 $ 15\varepsilon_{k} $
3 加劲板宜采用部分熔透焊缝焊接，主管为方管的加劲板靠支管一边与两侧边宜采用部分熔透焊接，与支管连接反向一边可不焊接。
4 当主管直径较小，加劲板的焊接必须断开主管钢管时，主管的拼接焊缝宜设置在距支管相贯焊缝最外侧冠点80mm以外处（图13.2.3-1（c））。
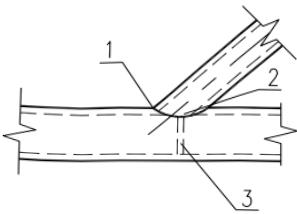
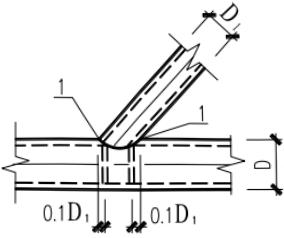
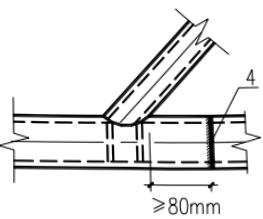
1—冠点；2—鞍点；3—加劲板；4—主管拼缝
1—内加劲板
13.2.4 钢管直接焊接节点采用主管表面贴加强板的方法加强时，应符合下列规定：
1 主管为圆管时，加强板宜包覆主管半圆（图 13.2.4（a）），长度方向两侧均应超过支管最外侧焊缝 50mm 以上，但不宜超过支管直径的 2/3，加强板厚度不宜小于 4mm。
2 主管为方（矩）形管且在与支管相连表面设置加强板（图 13.2.4（b））时，加强板长度 $ l_{p} $ 可按下列公式确定，加强板宽度 $ b_{p} $ 宜接近主管宽度，并预留适当的焊缝位置，加强板厚度不宜小于支管最大厚度的2倍。
T、Y 和 X 形节点
$$ l_{\mathrm{p}}\geq\frac{h_{\mathrm{l}}}{\sin\theta_{\mathrm{l}}}+\sqrt{b_{\mathrm{p}}(b_{\mathrm{p}}-b_{\mathrm{l}})} $$
K形间隙节点
$$ l_{\mathrm{p}}\geq1.5\left(\frac{h_{1}}{\sin\theta_{1}}+a+\frac{h_{2}}{\sin\theta_{2}}\right) $$
式中： $ l_{p} $ 、 $ b_{p} $ ——加强板的长度和宽度（mm）；
$ h_{1} $ 、 $ h_{2} $ ——支管1、2的截面高度（mm）；
$ b_{1} $ ——支管1的截面宽度（mm）；
$ \theta_{1} $ 、 $ \theta_{2} $ ——支管1、2轴线和主管轴线的夹角；
a——两支管在主管表面的距离（mm）。
3 主管为方（矩）形管且在与主管两侧表面设置加强板（图 13.2.4c）时，K形间隙节点：加强板长度 $ l_{p} $ 可按式（13.2.4-2）确定，T和Y形节点的加强板长度 $ l_{p} $ 可按下式确定：
$$ l_{\mathrm{p}}\geq\frac{1.5h_{\mathrm{l}}}{\sin\theta_{\mathrm{l}}} $$
4 加强板与主管应采用四周围焊。对 K、N 形节点焊缝有效高度不应小于腹杆壁厚。焊接前宜在加强板上先钻一个排气小孔，焊后应用塞焊将孔封闭。
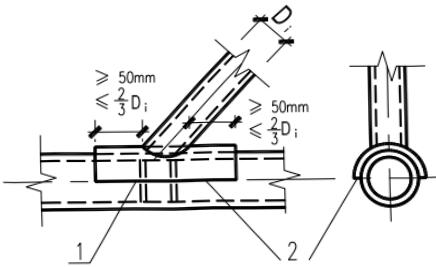
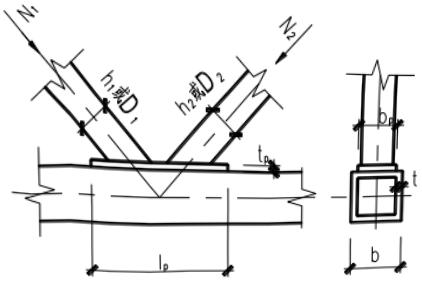
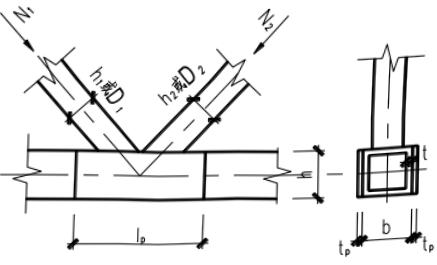
1—四周围焊；2—腹板
13.3 圆钢管直接焊接节点和局部加劲节点的计算
13.3.1 采用本节进行计算时，圆钢管连接节点应符合下列规定：
1 支管与主管外径及壁厚之比均不得小于 0.2，且不得大于 1.0；
2 主管外径与其壁厚之比不得大于 100;
3 支管外径与其壁厚之比不得大于 60;
4 主支管轴线间小于直角的夹角不得小于 $ 30^{\circ} $ ;
5 支管轴线在主管横截面所在平面投影的夹角不得小于 $ 60^{\circ} $ ，且不得大于 $ 120^{\circ} $ 。
13.3.2 无加劲直接焊接的平面节点，当支管按仅承受轴心力的构件设计时，平面节点的承载力设计值应按下列规定计算，支管在节点处的承载力设计值不得小于其轴心力设计值。
1 平面 X 形节点（图 13.3.2-1）：
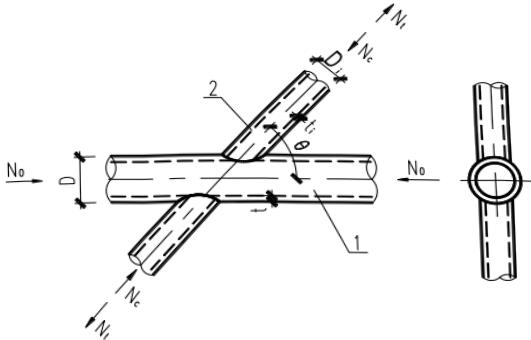
1—主管；2—支管
1）受压支管在管节点处的承载力设计值 $ N_{ex} $ 应按下列公式计算：
$$ N_{\mathrm{cX}}=\frac{5.45}{(1-0.81\beta)\sin\theta}\psi_{\mathrm{n}}t^{2}f $$
$$ \beta=D_{i}/D $$
$$ \psi_{\mathrm{n}}=1-0.3\frac{\sigma}{f_{\mathrm{y}}}-0.3\left(\frac{\sigma}{f_{\mathrm{y}}}\right)^{2} $$
式中： $ \psi_{n} $ ——参数，当节点两侧或者一侧主管受拉时，取 $ \psi_{n}=1 $ ，其余情况按式(13.3.2-3)计算；
t ——主管壁厚（mm）;
f——主管钢材的抗拉、抗压和抗弯强度设计值（N/mm²）；
$ \theta $ ——主支管轴线间小于直角的夹角；
D、 $ D_{i} $ ——分别为主管和支管的外径（mm）；
$ f_{y} $ ——主管钢材的屈服强度（N/mm $ ^{2} $ ）；
$ \sigma $ ——节点两侧主管轴心压应力的较小绝对值（N/mm $ ^{2} $ ）。
2）受拉支管在管节点处的承载力设计值 $ N_{tx} $ 应按下式计算：
$$ N_{\mathrm{tX}}=0.78\bigg(\frac{D}{t}\bigg)^{0.2}N_{\mathrm{cX}} $$
2 平面 T 形（或 Y 形）节点（图 13.3.2-2 和图 13.3.2-3）：
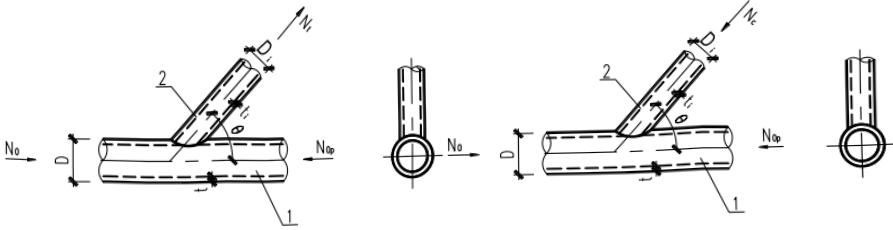
1—主管；2—支管 1—主管；2—支管
1）受压支管在管节点处的承载力设计值 $ N_{cT} $ 应按下式计算：
$$ N_{\mathrm{c T}}=\frac{11.51}{\sin\theta}\bigg(\frac{D}{t}\bigg)^{0.2}\psi_{\mathrm{n}}\psi_{\mathrm{d}}t^{2}f $$
当 $ \beta\leq0.7 $ 时：
$$ \psi_{\mathrm{d}}=0.069+0.93\beta $$
当 $ \beta>0.7 $ 时：
$$ \psi_{\mathrm{d}}=2\beta-0.68 $$
2）受拉支管在管节点处的承载力设计值 $ N_{t} $ 应按下列公式计算：
当 $ \beta\leq0.6 $ 时：
$$ N_{\mathrm{tT}}=1.4N_{cT} $$
当 $ \beta>0.6 $ 时：
$$ N_{\mathrm{t T}}=\big(2-\beta\big)N_{\mathrm{c T}} $$
3 平面 K 形间隙节点（图 13.3.2-4）：
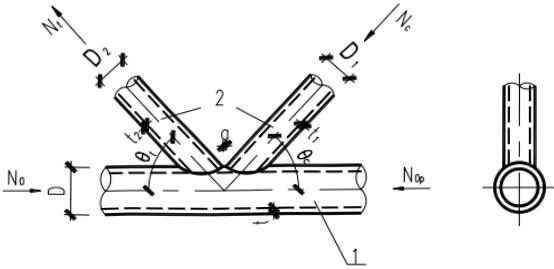
1—主管；2—支管
1）受压支管在管节点处的承载力设计值 $ N_{cK} $ 应按下列公式计算：
$$ N_{\mathrm{cK}}=\frac{11.51}{\sin\theta_{\mathrm{c}}}\bigg(\frac{D}{t}\bigg)^{0.2}\psi_{\mathrm{n}}\psi_{\mathrm{d}}\psi_{\mathrm{a}}t^{2}f $$
$$ \psi_{\mathrm{a}}=1+\left(\frac{2.19}{1+7.5a/D}\right)\left(1-\frac{20.1}{6.6+D/t}\right)\left(1-0.77\beta\right) $$
式中： $ \theta_{c} $ ——受压支管轴线与主管轴线的夹角；
$ \psi_{a} $ ——参数，按式(13.3.2-11)计算；
$ \psi_{d} $ ——参数，按式(13.3.2-6)或(13.3.2-7)计算；
a——两支管之间的间隙（mm）。
2）受拉支管在管节点处的承载力设计值 $ N_{tK} $ 应按下式计算：
$$ N_{\mathrm{tK}}=\frac{\sin\theta_{\mathrm{c}}}{\sin\theta_{\mathrm{t}}}N_{\mathrm{cK}} $$
式中： $ \theta_{t} $ ——受拉支管轴线与主管轴线的夹角。
4 平面 K 形搭接节点（图 13.3.2-5）：
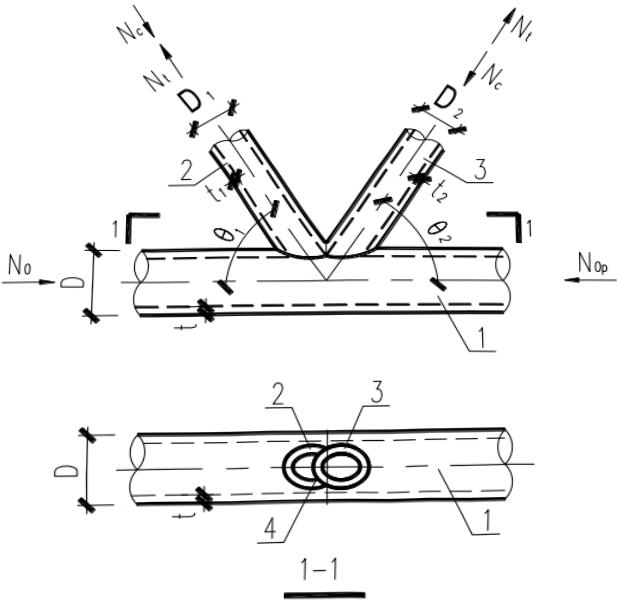
1—主管；2—搭接支管；3—被搭接支管；4—被搭接支管内隐藏部分
支管在管节点处的承载力设计值应按下列公式计算：
受压支管
$$ N_{\mathrm{cK}}=\left(\frac{29}{\psi_{\mathrm{q}}+25.2}-0.074\right)A_{\mathrm{c}}f $$
受拉支管
$$ N_{\mathrm{tK}}=\left(\frac{29}{\psi_{\mathrm{q}}+25.2}-0.074\right)A_{\mathrm{t}}f $$
$$ \psi_{\mathrm{q}}=\beta^{\eta_{\mathrm{o v}}}\gamma\tau^{0.8-\eta_{\mathrm{o v}}} $$
$$ \gamma=D/(2t) $$
$$ \tau=t_{i}/t $$
式中： $ \psi_{q} $ ——参数；
$ A_{c} $ ——受压支管的截面面积（mm $ ^{2} $ ）；
$ A_{t} $ ——受拉支管的截面面积（mm $ ^{2} $ ）；
f ——支管钢材的强度设计值（N/mm²）；
$ t_{i} $ ——支管壁厚（mm）；
$ N_{cK} $ ——受压支管在管节点处的承载力设计值（N）；
$ N_{tK} $ ——受拉支管在管节点处的承载力设计值（N）。
5 平面 DY 形节点（图 13.3.2-6）：
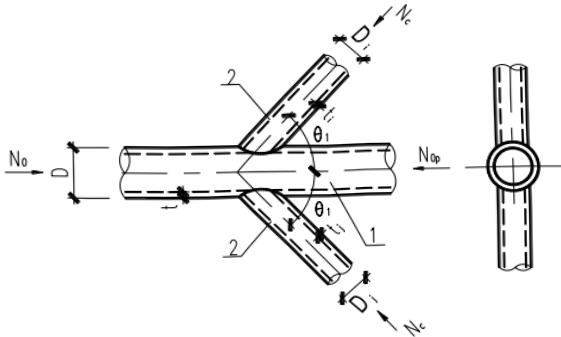
1—主管；2—支管
两受压支管在管节点处的承载力设计值 $ N_{cDY} $ 应按下式计算：
$$ N_{\mathrm{cDY}}=N_{\mathrm{cX}} $$
式中： $ N_{cX} $ ——X形节点中受压支管极限承载力设计值（N）。
6 平面 DK 形节点：
1）荷载正对称节点（图 13.3.2-7）：
四支管同时受压时，支管在管节点处的承载力应按下列公式验算：
$$ N_{1}\sin\theta_{1}+N_{2}\sin\theta_{2}\leq N_{\mathrm{cX}i}\sin\theta_{i} $$
$$ N_{cXi}\sin\theta_{i}=MAX\big(N_{cX1}\sin\theta_{1},N_{cX2}\sin\theta_{2}\big) $$
四支管同时受拉时，支管在管节点处的承载力应按下列公式验算：
$$ N_{{1}}\sin\theta{{1}}+N{{2}}\sin\theta{{2}}\leq N{tXi}\sin\theta_{_{i}} $$
$$ N_{\mathrm{tX}i}\sin\theta_{i}=\mathrm{MAX}\big(N_{\mathrm{tX}1}\sin\theta_{1},N_{\mathrm{tX}2}\sin\theta_{2}\big) $$
式中： $ N_{cX1}, N_{cX2} $ —— X 形节点中支管受压时节点承载力设计值（N）；
$ N_{tX1}, N_{tX2} $ —— X 形节点中支管受拉时节点承载力设计值（N）。
2）荷载反对称节点（图 13.3.2-8）：
$$ N_{1}\leq N_{\mathrm{cK}} $$
$$ N_{2}\leq N_{\mathrm{uK}} $$
对于荷载反对称作用的间隙节点（图 13.3.2-8），还需补充验算截面 a-a 的塑性剪切承载力：
$$ \sqrt{\left(\frac{\sum N_{i}\sin\theta_{i}}{V_{\mathrm{p}1}}\right)^{2}+\left(\frac{N_{\mathrm{a}}}{N_{\mathrm{p}1}}\right)^{2}}\leq1.0 $$
$$ V_{\mathrm{p1}}=\frac{2}{\pi}Af_{\mathrm{v}} $$
$$ N_{\mathrm{p1}}=\pi\big(D-t\big)tf $$
式中： $ N_{cK} $ ——平面 K 形节点中受压支管承载力设计值（N）；
$ N_{tK} $ ——平面 K 形节点中受拉支管承载力设计值（N）；
$ V_{p1} $ ——主管剪切承载力（N）；
A——主管截面面积（mm²）；
$ f_{v} $ ——主管钢材抗剪强度设计值（N/mm²）；
$ N_{p1} $ ——主管轴向承载力（N）；
$ N_{a} $ ——截面 a-a 处主管轴力设计值（N）。
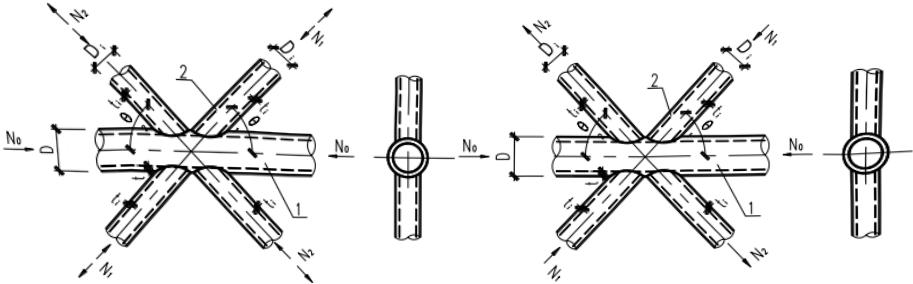
1—主管；2—支管 1—主管；2—支管
7 平面 KT 形（图 13.3.2-9）：
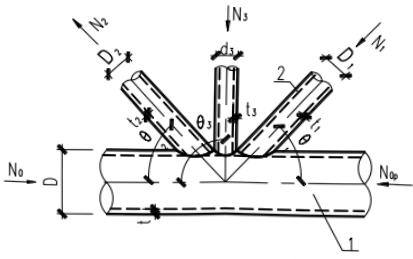
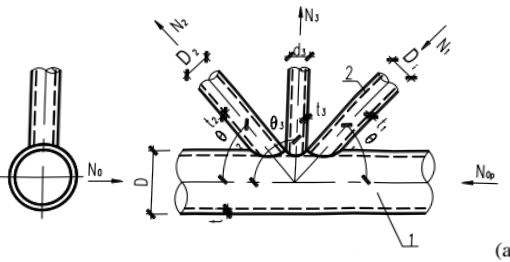
1—主管；2—支管
对有间隙的 KT 形节点，当竖杆不受力，可按没有竖杆的 K 形节点计算，其间隙值 a 取为两斜杆的趾间距；当竖杆受压力时，可按下列公式计算：
$$ N_{1}\sin\theta_{1}+N_{3}\sin\theta_{3}\leq N_{\mathrm{cK1}}\sin\theta_{1} $$
$$ N_{{2}}\sin\theta{{2}}\leq N{{cK1}}\sin\theta{_{1}} $$
当竖杆受拉力时，尚应按下式计算：
$$ N_{\mathrm{i}}\leq N_{\mathrm{cKl}} $$
式中： $ N_{cK1} $ —— K 形节点支管承载力设计值，由式(13.3.2-11)计算，式(13.3.2-11)中
$ \beta=\left(D_{1}+D_{2}+D_{3}\right)/3D $ ，a为受压支管与受拉支管在主管表面的间隙。
8 T、Y、X形和有间隙的K、N形、平面KT形节点的冲剪验算，支管在节点处的冲剪承载力设计值 $ N_{si} $ 应按下式进行补充验算：
$$ N_{\mathrm{s}i}=\pi\frac{1+\sin\theta_{i}}{2\sin^{2}\theta_{i}}t D_{i}f_{\mathrm{v}} $$
13.3.3 无加劲直接焊接的空间节点，当支管按仅承受轴力的构件设计时，空间节点的承载力设计值应按下列规定计算，支管在节点处的承载力设计值不得小于其轴心力设计值。
1 空间 TT 形节点（图 13.3.3-1）：
1）受压支管在管节点处的承载力设计值 $ N_{cTT} $ 应按下列公式计算：
$$ N_{\mathrm{cTT}}=\psi_{\mathrm{ao}}N_{\mathrm{cT}} $$
$$ \psi_{ao}=1.28-0.64\frac{a_{o}}{D}\leq1.1 $$
式中： $ a_{0} $ ——两支管的横向间隙。
2）受拉支管在管节点处的承载力设计值 $ N_{TT} $ 应按下式计算：
$$ N_{\mathrm{tTT}}=N_{\mathrm{cTT}} $$
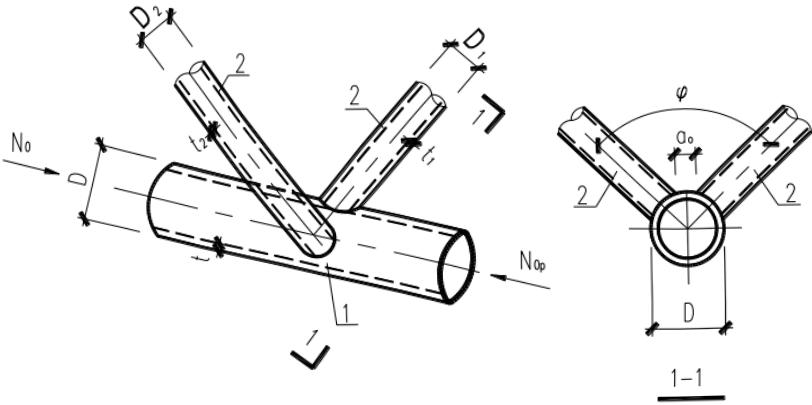
1—主管；2—支管
2 空间 KK 形节点（图 13.3.3-2）：
受压或受拉支管在空间管节点处的承载力设计值 $ N_{cKK} $ 或 $ N_{tKK} $ 应分别按平面 K 形节点相应支管承载力设计值 $ N_{cK} $ 或 $ N_{tK} $ 乘以空间调整系数 $ \mu_{KK} $ 计算。
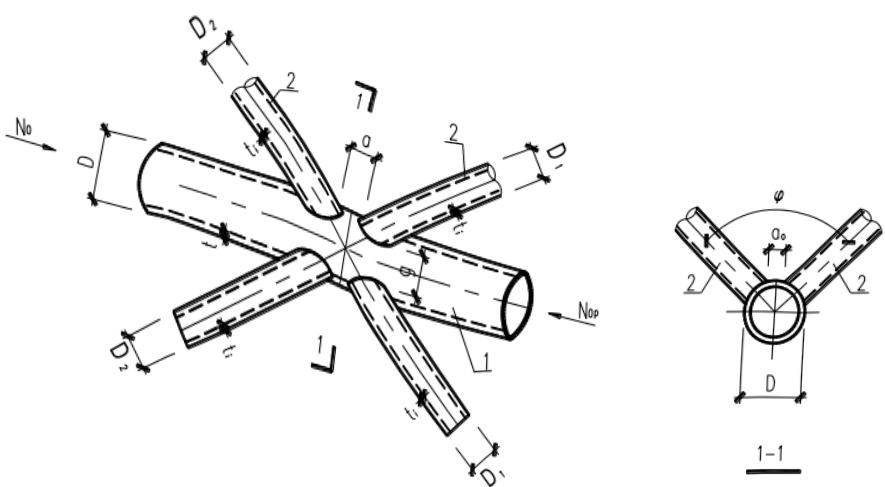
1—主管；2—支管
支管为非全搭接型
$$ \mu_{\mathrm{KK}}=0.9 $$
支管为全搭接型
$$ \mu_{\mathrm{KK}}=0.74\gamma^{0.1}\exp\left(0.6\zeta_{\mathrm{t}}\right) $$
$$ \zeta_{t}=\frac{q_{0}}{D} $$
式中： $ \zeta_{t} $ ——参数；
$ q_{0} $ ——平面外两支管的搭接长度（mm）。
3 空间 KT 形圆管节点(图 13.3.3-3):
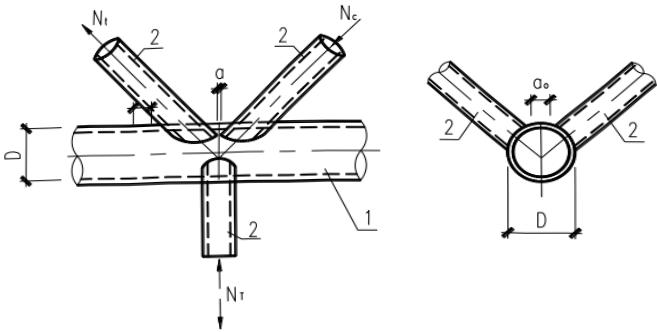
1—主管；2—支管
1）K形受压支管在管节点处的承载力设计值 $ N_{cKT} $ 应按下列公式计算：
$$ N_{\mathrm{cK T}}=Q_{\mathrm{n}}\mu_{\mathrm{K T}}N_{\mathrm{cK}} $$
$$ Q_{\mathrm{n}}=\frac{1}{1+\frac{0.7n_{\mathrm{TK}}^{2}}{1+0.6n_{\mathrm{TK}}}} $$
$$ n_{\mathrm{TK}}=N_{\mathrm{T}}\big/\big|N_{\mathrm{cK}}\big| $$
$$ \mu_{KT}=\begin{cases}1.15\beta_{T}^{0.07}\exp\left(-0.2\zeta_{o}\right)& 空间 KT 形间隙节点 \1.0& 空间 KT 形平面内搭接节点 \0.74\gamma^{0.1}\exp\left(-0.25\zeta_{o}\right)& 空间 KT 形全搭接节点 \end{cases} $$
$$ \zeta_{0}=\frac{a_{0}}{D} 或 \frac{q_{0}}{D} $$
2）K形受拉支管在管节点处的承载力设计值 $ N_{KT} $ 应按下式计算：
$$ N_{\mathrm{tKT}}=Q_{\mathrm{n}}\mu_{\mathrm{KT}}N_{\mathrm{tK}} $$
3）T形支管在管节点处的承载力设计值 $ N_{KT} $ 应按下式计算：
$$ N_{\mathrm{KT}}=n_{\mathrm{TK}}N_{\mathrm{cKT}} $$
式中： $ Q_{n} $ ——支管轴力比影响系数；
$ n_{TK} $ ——支管轴心力比，按式（13.3.3-11）计算， $ -1 \leq n_{TK} \leq 1 $ 。
$ N_{T} $ 、 $ N_{cK} $ ——分别为T形支管和K形受压支管的轴力设计值(N)，以拉为正，以压为负(N)；
$ \mu_{KT} $ ——空间调整系数，根据图 13.3.3-4 的支管搭接方式分别取值；
$ \beta_{T} $ ——T形支管与主管的直径比；
$ \zeta_{0} $ ——参数；
$ a_{o} $ ——K形支管与T形支管的平面外间隙（mm）；
$ q_{o} $ ——K形支管与T形支管的平面外搭接长度（mm）。
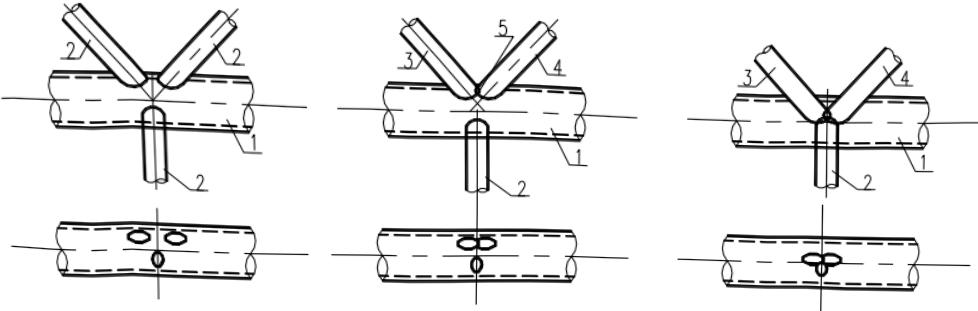
1—主管；2—支管；3—贯通支管；4—搭接支管；5—内隐蔽部分
13.3.4 无加劲直接焊接的平面 T、Y、X 形节点，当支管承受弯矩作用时（图 13.3.4-1 和图 13.3.4-2），节点承载力应按下列规定计算：
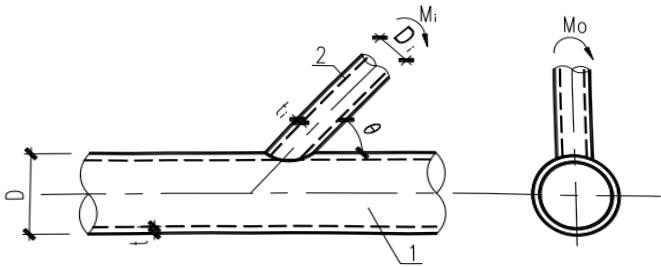
1—主管；2—支管
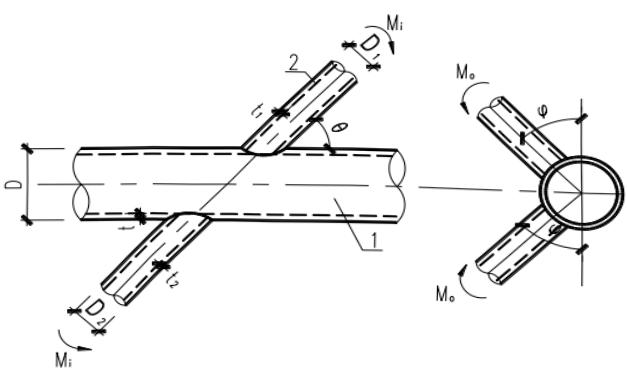
1—主管；2—支管
1 支管在管节点处的平面内受弯承载力设计值 $ M_{iT} $ 应按下列公式计算（图 13.3.4-2）：
$$ M_{\mathrm{iT}}=Q_{\mathrm{x}}Q_{\mathrm{f}}\frac{D_{i}t^{2}f}{\sin\theta_{i}} $$
$$ Q_{x}=6.09\beta\gamma^{0.42} $$
当节点两侧或一侧主管受拉时：
$$ Q_{\mathrm{f}}=1 $$
当节点两侧主管受压时：
$$ Q_{\mathrm{f}}=1-0.3n_{\mathrm{p}}-0.3n_{\mathrm{p}}^{2} $$
$$ n_{\mathrm{p}}=\frac{N_{\mathrm{op}}}{Af_{\mathrm{y}}}+\frac{M_{\mathrm{op}}}{Wf_{\mathrm{y}}} $$
当 $ D_{i}\leq D-2t $ 时，平面内弯矩不应大于下式规定的抗冲剪承载力设计值：
$$ M_{\mathrm{s i T}}=\left(\frac{1+3\sin\theta_{i}}{4\sin^{2}\theta_{i}}\right)D_{i}^{2}t f_{\mathrm{v}} $$
式中： $ Q_{x} $ ——参数；
$ Q_{f} $ ——参数；
$ N_{op} $ ——节点两侧主管轴心压力的较小绝对值（N）；
$ M_{op} $ ——节点与 $ N_{op} $ 对应一侧的主管平面内弯矩绝对值（N·mm）；
A——与 $ N_{op} $ 对应一侧的主管截面积（mm $ ^{2} $ ）；
W——与 $ N_{op} $ 对应一侧的主管截面模量（mm $ ^{3} $ ）。
2 支管在管节点处的平面外受弯承载力设计值 $ M_{oT} $ 应按下列公式计算：
$$ M_{\mathrm{oT}}=Q_{\mathrm{y}}Q_{\mathrm{f}}\frac{D_{i}t^{2}f}{\sin\theta} $$
$$ Q_{\mathrm{y}}=3.2\gamma^{\left(0.5\beta^{2}\right)} $$
当 $ D_{i}\leq D-2t $ 时，平面外弯矩不应大于下式规定的抗冲剪承载力设计值：
$$ M_{\mathrm{s o T}}=\left(\frac{3+\sin\theta}{4\sin^{2}\theta}\right)D_{i}^{2}t f_{\mathrm{v}} $$
3 支管在平面内、外弯矩和轴力组合作用下的承载力应按下式验算：
$$ \frac{N}{N_{{j}}}+\frac{M{{i}}}{M{{iT}}}+\frac{M{{o}}}{M{_{oT}}}\leq1.0 $$
式中：N、 $ M_{i} $ 、 $ M_{o} $ ——支管在管节点处的轴心力、平面内弯矩、平面外弯矩设计值；
$ N_{j} $ ——支管在管节点处的承载力设计值，根据节点形式按本标准第13.3.2条的规定计算。
13.3.5 主管呈弯曲状的平面或空间圆管焊接节点，当主管曲率半径 $ R \geq 5m $ 且主管曲率半径 R 与主管直径 D 之比不小于 12 时，可采用本标准第 13.3.2 条和第 13.3.4 条所规定的计算公式进行承载力计算。
13.3.6 主管采用本标准第 13.2.4 条第 1 款外贴加强板方式的节点：当支管受压时，节点承载力设计值取相应未加强时节点承载力设计值的 $ \left(0.23\tau_{r}^{1.18}\beta^{-0.68}+1\right) $ 倍；当支管受拉时，节点承载力设计值取相应未加强时节点承载力设计值的 $ 1.13\tau_{r}^{0.59} $ 倍； $ \tau_{r} $ 为加强板厚度与主管壁厚的比值。
13.3.7 支管为方（矩）形管的平面 T、X 形节点，支管在节点处的承载力应按下列规定计算：
1 T形节点：
1）支管在节点处的轴向承载力设计值应按下式计算：
$$ N_{\mathrm{TR}}=\left(4+20\beta_{\mathrm{RC}}^{2}\right)\left(1+0.25\eta_{\mathrm{RC}}\right)\psi_{\mathrm{n}}t^{2}f $$
$$ \beta_{\mathrm{RC}}=\frac{b_{1}}{D} $$
$$ \eta_{\mathrm{RC}}=\frac{h_{1}}{D} $$
2）支管在节点处的平面内受弯承载力设计值应按下式计算：
$$ M_{\mathrm{i T R}}=h_{\mathrm{1}}N_{\mathrm{T R}} $$
3）支管在节点处的平面外受弯承载力设计值应按下式计算：
$$ M_{\mathrm{o T R}}=0.5b_{\mathrm{l}}N_{\mathrm{T R}} $$
式中： $ \beta_{RC} $ ——支管的宽度与主管直径的比值，且需满足 $ \beta_{RC}\geq0.4 $ ；
$ \eta_{RC} $ ——支管的高度与主管直径的比值，且需满足 $ \eta_{RC}\leq4 $ ;
$ b_{1} $ ——支管的宽度（mm）；
$ h_{1} $ ——支管的平面内高度（mm）；
t——主管壁厚（mm）；
f——主管钢材的抗拉、抗压和抗弯强度设计值（N/mm²）。
2 X形节点：
1）节点轴向承载力设计值应按下式计算：
$$ N_{\mathrm{XR}}=\frac{5\left(1+0.25\eta_{\mathrm{RC}}\right)}{1-0.81\beta_{\mathrm{RC}}}\psi_{\mathrm{n}}t^{2}f $$
2）节点平面内受弯承载力设计值应按下式计算：
$$ M_{\mathrm{i X R}}=h_{i}N_{\mathrm{X R}} $$
3）节点平面外受弯承载力设计值应按下式计算：
$$ M_{\mathrm{o X R}}=0.5b_{i}N_{\mathrm{X R}} $$
3 节点尚应按下式进行冲剪计算：
$$ \sigma_{\max}t_{1}=\left(N_{1}/A_{1}+M_{\mathrm{x}1}/W_{\mathrm{x}1}+M_{\mathrm{y}1}/W_{\mathrm{y}1}\right)t_{1}\leq t f_{\mathrm{v}} $$
式中： $ N_{1} $ ——支管的轴向力（N）；
$ A_{1} $ ——支管的横截面积（mm $ ^{2} $ ）；
$ M_{x1} $ ——支管轴线与主管表面相交处的平面内弯矩（N·mm）;
$ W_{x1} $ ——支管轴线与主管表面相交处的平面内弹性抗弯截面模量（mm $ ^{3} $ ）；
$ M_{v1} $ ——支管轴线与主管表面相交处的平面外弯矩（N·mm）；
$ W_{y1} $ ——支管轴线与主管表面相交处的平面外弹性抗弯截面模量（mm $ ^{3} $ ）；
$ t_{1} $ ——支管壁厚（mm）；
$ f_{v} $ ——主管钢材的抗剪强度设计值（N/mm²）。
13.3.8 在节点处，支管沿周边与主管相焊；支管互相搭接处，搭接支管沿搭接边与被搭接支管相焊。焊缝承载力不应小于节点承载力。
13.3.9 T（Y）、X 或 K 形间隙节点及其他非搭接节点中，支管为圆管时的焊缝承载力设计值应按下列规定计算：
1 支管仅受轴力作用时：
非搭接支管与主管的连接焊缝可视为全周角焊缝进行计算。角焊缝的计算厚度沿支管周长取 $ 0.7h_{f} $ ，焊缝承载力设计值 $ N_{f} $ 可按下列公式计算：
$$ N_{\mathrm{f}}=0.7h_{\mathrm{f}}l_{\mathrm{w}}f_{\mathrm{f}}^{\mathrm{w}} $$
当 $ D_{i}/D \leq 0.65 $ 时：
$$ l_{\mathrm{w}}=\left(3.25D_{i}-0.025D\right)\left(\frac{0.534}{\sin\theta_{i}}+0.446\right) $$
当 $ 0.65<D_{i}/D\leq1 $ 时：
$$ l_{\mathrm{w}}=\left(3.81D_{i}-0.389D\right)\left(\frac{0.534}{\sin\theta_{i}}+0.446\right) $$
式中： $ h_{f} $ ——焊脚尺寸（mm）；
$ f_{f}^{w} $ ——角焊缝的强度设计值（N/mm $ ^{2} $ ）；
$ l_{w} $ ——焊缝的计算长度（mm）。
2 平面内弯矩作用下：
支管与主管的连接焊缝可视为全周角焊缝进行计算。角焊缝的计算厚度沿支管周长取 $ 0.7h_{f} $ ，焊缝承载力设计值 $ M_{fi} $ 可按下列公式计算：
$$ M_{\mathrm{f i}}=W_{\mathrm{f i}}f_{\mathrm{f}}^{\mathrm{w}} $$
$$ W_{\mathrm{fi}}=\frac{I_{\mathrm{fi}}}{x_{\mathrm{c}}+D/\left(2\sin\theta_{i}\right)} $$
$$ x_{c}=\left(-0.34\sin\theta_{i}+0.34\right)\cdot\left(2.188\beta^{2}+0.059\beta+0.188\right)\cdot D_{i} $$
$$ I_{\mathrm{fi}}=\left(\frac{0.826}{\sin^{2}\theta}+0.113\right)\cdot\left(1.04+0.124\beta-0.322\beta^{2}\right)\cdot\frac{\pi}{64}\cdot\frac{\left(D+1.4h_{\mathrm{f}}\right)^{4}-D^{4}}{\cos\phi_{\mathrm{fi}}} $$
$$ \phi_{f i}=\arcsin\left(D_{i}/D\right)=\arcsin\beta $$
式中： $ W_{fr} $ ——焊缝有效截面的平面内抗弯模量，按式(13.3.9-5)计算（mm $ ^{3} $ ）；
$ x_{c} $ ——参数，按式(13.3.9-6)计算（mm）：
$ I_{fr} $ ——焊缝有效截面的平面内抗弯惯性矩，按式(13.3.9-7)计算 $ \left(\mathrm{mm}^{4}\right) $ 。
3 平面外弯矩作用下：
支管与主管的连接焊缝可视为全周角焊缝进行计算。角焊缝的计算厚度沿支管周长取 $ 0.7h_{f} $ ，焊缝承载力设计值 $ M_{f0} $ 可按下列公式计算：
$$ M_{\mathrm{f o}}=W_{\mathrm{f o}}f_{\mathrm{f}}^{\mathrm{w}} $$
$$ W_{\mathrm{f o}}=\frac{I_{\mathrm{f o}}}{D/\left(2\cos\phi_{\mathrm{f o}}\right)} $$
$$ \phi_{\mathrm{f o}}=\arcsin\left(D_{i}/D\right)=\arcsin\beta $$
$$ I_{\mathrm{f o}}=\left(0.26\sin\theta+0.74\right)\cdot\left(1.04-0.06\beta\right)\cdot\frac{\pi}{64}\cdot\frac{\left(D+1.4h_{\mathrm{f}}\right)^{4}-D^{4}}{\cos^{3}\phi_{\mathrm{f o}}} $$
式中： $ W_{fo} $ ——焊缝有效截面的平面外抗弯模量，按式(13.3.9-10)计算（mm $ ^{3} $ ）；
$ I_{fo} $ ——焊缝有效截面的平面外抗弯惯性矩，按式(13.3.9-12)计算（mm $ ^{4} $ ）。
13.4 矩形钢管直接焊接节点和局部加劲节点的计算
13.4.1 本节规定适用于直接焊接且主管为矩形管，支管为矩形管或圆管的钢管节点（图13.4.1），其适用范围应符合表13.4.1的要求。
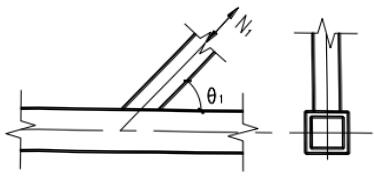
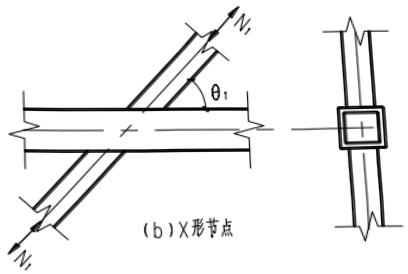
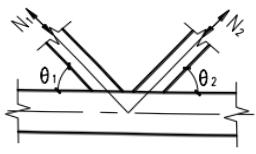
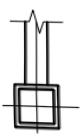
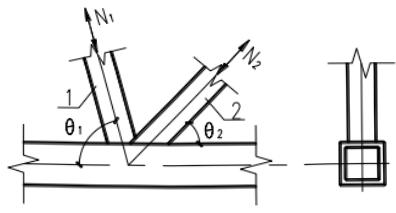
1—搭接支管；2—被搭接支管
| 截面及节点形式 | 节点几何参数,i=1或2,表示支管;j表示被搭接支管 | ||||||
| b1/b2/b3/b4 | b1/b2/b3/b4 | b1/b2/b3/b4 | b1/b2/b3/b4 | b1/b2/b3/b4 | a或ηovb1/b2/b3/b4 | ||
| 受压 | 受拉 | ||||||
| 支 | T、Y与X | ≥0.25 | ≤37εk,i | ≤35 | 0.5≤h1/b1≤2.0 | ≤35 | — |
| 管为矩形管 | K与N间隙节点 | ≥0.1+0.01b/tβ≥0.35 | 且≤35 | 0.5(1-β)≤a/b≤1.5(1-β)25%≤ηov≤100%a≥t1+t2 | |||
| K与N搭接节点 | ≥0.25 | ≤33εk,i | ≤40 | t1≤1.0t2≤b/b1≤1.0 | |||
| 支管为圆管 | 0.4≤D/b≤0.8 | ≤44εk,i | ≤50 | 取b1=D1仍能满足上述相应条件 | |||
注：1 当 $ \frac{a}{b}>1.5(1-\beta) $ ，则按 T 形或 Y 形节点计算。
2 $ b_{i} $ 、 $ h_{i} $ 、 $ t_{i} $ 分别为第 i 个矩形支管的截面宽度、高度和壁厚； $ D_{i} $ 、 $ t_{i} $ 分别为第 i 个圆支管的外径和壁厚；b、h、t 为矩形主管的截面宽度、高度和壁厚；a 为支管间的间隙； $ \eta_{ov} $ 为搭接率； $ \varepsilon_{k,i} $ 为第 i 个支管钢材的钢号调整系数； $ \beta $ 为参数：对 T、Y、X 形节点， $ \beta=\frac{b_{1}}{b} $ 或 $ \frac{D_{1}}{b} $ ；对 K、N 形节点， $ \beta=\frac{b_{1}+b_{2}+h_{1}+h_{2}}{4b} $ 或 $ \beta=\frac{D_{1}+D_{2}}{b} $ 。
13.4.2 无加劲直接焊接的平面节点，当支管按仅承受轴心力的构件设计时，平面节点的承载力设计值应按下列规定计算，支管在节点处的承载力设计值不得小于其轴心力设计值。
1 支管为矩形管的平面 T、Y 和 X 形节点：
1）当 $ \beta \leq 0.85 $ 时，支管在节点处的承载力设计值 $ N_{ui} $ 应按下列公式计算：
$$ N_{\mathrm{u}i}=1.8\left(\frac{h_{i}}{bC\sin\theta_{i}}+2\right)\frac{t^{2}f}{C\sin\theta_{i}}\psi_{\mathrm{n}} $$
$$ C=\left(1-\beta\right)^{0.5} $$
主管受压时：
$$ \psi_{\mathrm{n}}=1.0-\frac{0.25\sigma}{\beta f} $$
主管受拉时：
$$ \psi_{n}=1.0 $$
式中：C ——参数，按式(13.4.2-2)计算；
$ \psi_{n} $ ——参数，按式(13.4.2-3)或式(13.4.2-4)计算；
$ \sigma $ ——节点两侧主管轴心压应力的较大绝对值（N/mm $ ^{2} $ ）。
2）当 $ \beta=1.0 $ 时，支管在节点处的承载力设计值 $ N_{ui} $ 应按下式计算：
$$ N_{\mathrm{u}i}=\left(\frac{2h_{i}}{\sin\theta_{i}}+10t\right)\frac{tf_{\mathrm{k}}}{\sin\theta_{i}}\psi_{\mathrm{n}} $$
对于 X 形节点，当 $ \theta_{i} < 90^{\circ} $ 且 $ h \geq h_{i} / \cos \theta_{i} $ 时，尚应按下式计算：
$$ N_{\mathrm{u}i}=\frac{2htf_{\mathrm{v}}}{\sin\theta_{i}} $$
当支管受拉时：
$$ f_{\mathrm{k}}=f $$
当支管受压时：
对 T、Y 形节点：
$$ f_{\mathrm{k}}=0.8\varphi f $$
对 X 形节点：
$$ f_{\mathrm{k}}=\left(0.65\sin\theta_{i}\right)\varphi f $$
$$ \lambda=1.73\left(\frac{h}{t}-2\right)\sqrt{\frac{1}{\sin\theta_{i}}} $$
式中： $ f_{v} $ ——主管钢材抗剪强度设计值（N/mm²）；
$ f_{k} $ ——主管强度设计值，按式(13.4.2-8)或式(13.4.2-9)计算（N/mm²）；
$ \varphi $ ——长细比按式(13.4.2-10)确定的轴心受压构件的稳定系数。
3）当 $ 0.85<\beta\leq1.0 $ 时，支管在节点处的承载力设计值 $ N_{ui} $ 应按式(13.4.2-1)、式(13.4.2-5)
所计算的值，根据 $ \beta $ 进行线性插值。此外，尚应不超过式(13.4.2-11)的计算值：
$$ N_{\mathrm{u}i}=2.0\big(h_{i}-2t_{i}+b_{\mathrm{e}i}\big)t_{i}f_{i} $$
$$ b_{ei}=\frac{10}{b/t}\cdot\frac{tf_{y}}{t_{i}f_{yi}}\cdot b_{i}\leq b_{i} $$
4）当 $ 0.85 \leq \beta \leq 1 - 2t/b $ 时， $ N_{ui} $ 尚应不超过下列公式的计算值：
$$ N_{\mathrm{u}i}=2.0\Bigg(\frac{h_{\mathrm{i}}}{\sin\theta_{\mathrm{i}}}+b_{\mathrm{e}i}^{\cdot}\Bigg)\frac{tf_{\mathrm{v}}}{\sin\theta_{\mathrm{i}}} $$
$$ b_{ei}^{^{\prime}}=\frac{10}{b/t}\cdot b_{i}\leq b_{i} $$
式中： $ f_{i} $ ——支管钢材抗拉（抗压和抗弯）强度设计值（N/mm $ ^{2} $ ）。
2 支管为矩形管的有间隙的平面 K 形和 N 形节点：
1）节点处任一支管的承载力设计值应取下列各式的较小值：
$$ N_{\mathrm{u}i}=\frac{8}{\sin\theta_{i}}\beta\bigg(\frac{b}{2t}\bigg)^{0.5}t^{2}f\psi_{\mathrm{n}} $$
$$ N_{\mathrm{u}i}=\frac{A_{\mathrm{v}}f_{\mathrm{v}}}{\sin\theta_{i}} $$
$$ N_{\mathrm{u}i}=2.0\Bigg(h_{i}-2t_{i}+\frac{b_{i}+b_{\mathrm{e}i}}{2}\Bigg)t_{i}f_{i} $$
当 $ \beta\leq1-2t/b $ 时，尚应不超过式(13.4.2-18)的计算值：
$$ N_{\mathrm{u}i}=2.0\Bigg(\frac{h_{i}}{\sin\theta_{i}}+\frac{b_{i}+b_{\mathrm{e}i}^{,}}{2}\Bigg)\frac{tf_{\mathrm{v}}}{\sin\theta_{i}} $$
$$ A_{\mathrm{v}}=\left(2h+\alpha b\right)t $$
$$ \alpha=\sqrt{\frac{3t^{2}}{3t^{2}+4a^{2}}} $$
式中： $ A_{v} $ ——主管的受剪面积，应按式(13.4.2-19)计算（mm $ ^{2} $ ）；
$ \alpha $ ——参数，应按式(13.4.2-20)计算，（支管为圆管时 $ \alpha=0 $ ）。
2）节点间隙处的主管轴心受力承载力设计值为：
$$ N=\left(A-\alpha_{\mathrm{v}}A_{\mathrm{v}}\right)f $$
$$ \alpha_{\mathrm{v}}=1-\sqrt{1-\left(\frac{V}{V_{\mathrm{p}}}\right)^{2}} $$
$$ V_{\mathrm{p}}=A_{\mathrm{v}}f_{\mathrm{v}} $$
式中： $ \alpha_{v} $ ——剪力对主管轴心承载力的影响系数，按式(13.4.2-22)计算；
V——节点间隙处弦杆所受的剪力，可按任一支管的竖向分力计算（N）；
A——主管横截面面积（mm $ ^{2} $ ）。
3 支管为矩形管的搭接的平面 K 形和 N 形节点：
搭接支管的承载力设计值应根据不同的搭接率 $ \eta_{ov} $ 按下列公式计算（下标j表示被搭接支管）：
1）当 $ 25\%\leq\eta_{ov}<50\% $ 时：
$$ N_{\mathrm{u}i}=2.0\Bigg[\big(h_{i}-2t\big)\frac{\eta_{\mathrm{ov}}}{0.5}+\frac{b_{\mathrm{ei}}+b_{\mathrm{ej}}}{2}\Bigg]t_{i}f_{i} $$
$$ b_{\mathrm{e}j}=\frac{10}{b_{j}/t_{j}}\cdot\frac{t_{j}f_{\mathrm{y}j}}{t_{i}f_{\mathrm{y}i}}\cdot b_{i}\leq b_{i} $$
2）当 $ 50\%\leq\eta_{ov}<80\% $ 时：
$$ N_{\mathrm{u}i}=2.0\Bigg(h_{i}-2t_{i}+\frac{b_{\mathrm{e}i}+b_{\mathrm{e}j}}{2}\Bigg)t_{i}f_{i} $$
3）当 $ 80\%\leq\eta_{ov}<100\% $ 时：
$$ N_{\mathrm{u}i}=2.0\Bigg(h_{i}-2t_{i}+\frac{b_{i}+b_{\mathrm{e}j}}{2}\Bigg)t_{i}f_{i} $$
被搭接支管的承载力应满足下式要求：
$$ \frac{N_{\mathrm{u}j}}{A_{j}f_{\mathrm{y}j}}\leq\frac{N_{\mathrm{u}i}}{A_{i}f_{\mathrm{y}i}} $$
4 支管为矩形管的平面 KT 形节点：
1) 当为间隙 KT 形节点时，若垂直支管内力为零，则假设垂直支管不存在，按 K 形节点计算。若垂直支管内力不为零，可通过对 K 形和 N 形节点的承载力公式进行修正来计算，此时 $ \beta \leq (b_{1} + b_{2} + b_{3} + h_{1} + h_{2} + h_{3}) / (6b) $ ，间隙值取为两根受力较大且力的符号相反（拉或压）的腹杆间的最大间隙。对于图 13.4.2（a）、（b）所示受荷情况（P 为节点横向荷载，可为零），应满足式(13.4.2-29)~式(13.4.2-31)的要求：
$$ N_{\mathrm{u}1}\sin\theta_{1}\geq N_{2}\sin\theta_{2}+N_{3}\sin\theta_{3} $$
$$ N_{\mathrm{u1}}\geq N_{\mathrm{l}} $$
$$ N_{\mathrm{u}1}\sin\theta_{1}=N_{\mathrm{u}2}\sin\theta_{2} $$
式中： $ N_{1} $ 、 $ N_{2} $ 、 $ N_{3} $ ——腹杆所受的轴向力（N）。
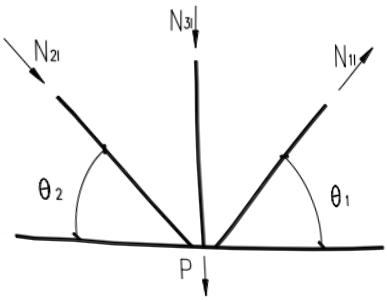
2) 当为搭接 KT 形方管节点时，可采用搭接 K 形和 N 形节点的承载力公式检验每一根支管的承载力。计算支管有效宽度时应注意支管搭接次序。
5 支管为圆管的各种形式平面节点：
支管为圆管的 T、Y、X、K 及 N 形节点时，支管在节点处的承载力可用上述相应的支管为矩形管的节点的承载力公式计算，这时需用 $ D_{i} $ 替代 $ b_{i} $ 和 $ h_{i} $ ，并将计算结果乘以 $ \pi/4 $ 。
13.4.3 无加劲直接焊接的 T 形方管节点，当支管承受弯矩作用时，节点承载力应按下列规定计算：
1 当 $ \beta\leq0.85 $ 且 $ n\leq0.6 $ 时，按式（13.4.3-1）验算；当 $ \beta\leq0.85 $ 且 n>0.6 时，按式（13.4.3-2）验算；当 $ \beta>0.85 $ 时，按式（13.4.3-2）验算。
$$ \left(\frac{N}{N_{\mathrm{u l}}^{*}}\right)^{2}+\left(\frac{M}{M_{\mathrm{u l}}}\right)^{2}\leq1.0 $$
$$ \frac{N}{N^{*}{ul}}+\frac{M}{M{u1}}\leq1.0 $$
式中： $ N_{ul}^{*} $ ——支管在节点处的轴心受压承载力设计值，应按本条第2款的规定计算（N）：
$ M_{u1} $ ——支管在节点处的受弯承载力设计值，应按本条第3款的规定计算（N·mm）。
2 $ N_{u1}^{*} $ 的计算应符合下列规定：
1) 当 $ \beta \leq 0.85 $ 时，按下式计算：
$$ N_{\mathrm{u}1}^{*}=t^{2}f\left[\frac{h_{1}/b}{1-\beta}\left(2-n^{2}\right)+\frac{4}{\sqrt{1-\beta}}\left(1-n^{2}\right)\right] $$
2) 当 $ \beta > 0.85 $ 时，按本标准第 13.4.2 条中的相关规定计算。
3 $ M_{u1} $ 的计算应符合下列规定：
当 $ \beta\leq0.85 $ 时：
$$ M_{\mathrm{u l}}=t^{2}h_{\mathrm{l}}f\left(\frac{b}{2h_{\mathrm{l}}}+\frac{2}{\sqrt{1-\beta}}+\frac{h_{\mathrm{l}}/b}{1-\beta}\right)\left(1-n^{2}\right) $$
$$ n=\frac{\sigma}{f} $$
当 $ \beta > 0.85 $ 时，其受弯承载力设计值取式（13.4.3-6）和（13.4.3-8）或（13.4.3-9）计算结果的较小值：
$$ M_{\mathrm{u l}}=\left[W_{\mathrm{l}}-\left(1-\frac{b_{\mathrm{e}}}{b}\right)b_{\mathrm{l}}t_{\mathrm{l}}\left(h_{\mathrm{l}}-t_{\mathrm{l}}\right)\right]f_{\mathrm{l}} $$
$$ b_{\mathrm{e}}=\frac{10}{b/t}\cdot\frac{tf_{\mathrm{y}}}{t_{\mathrm{1}}f_{\mathrm{y1}}}b_{\mathrm{l}}\leq b_{\mathrm{l}} $$
当 $ t \leq 2.75 mm $ :
$$ M_{\mathrm{u l}}=0.595t\left(h_{\mathrm{l}}+5t\right)^{2}\left(1-0.3n\right)f $$
当 $ t＞2.75mm $ :
$$ M_{\mathrm{u l}}=0.0025t\Big(t^{2}-26.8t+304.6\Big)\big(h_{\mathrm{l}}+5t\big)^{2}\big(1-0.3n\big)f $$
式中：n——参数，按式(13.4.3-5)计算，受拉时取n=0;
$ b_{e} $ ——腹杆翼缘的有效宽度，按式(13.4.3-7)计算（mm）；
$ W_{1} $ ——支管截面模量（mm $ ^{3} $ ）。
13.4.4 采用局部加强的方（矩）形管节点时，支管在节点加强处的承载力设计值应按下列规定计算：
1 主管与支管相连一侧采用加强板（图 13.2.4（b））：
1) 对支管受拉的 T、Y 和 X 形节点，支管在节点处的承载力设计值应按下列公式计算：
$$ N_{\mathrm{u}i}=1.8\left(\frac{h_{i}}{b_{\mathrm{p}}C_{\mathrm{p}}\sin\theta_{i}}+2\right)\frac{t_{\mathrm{p}}^{2}f_{\mathrm{p}}}{C_{\mathrm{p}}\sin\theta_{i}} $$
$$ C_{\mathrm{p}}=\left(1-\beta_{\mathrm{p}}\right)^{0.5} $$
$$ \beta_{\mathrm{p}}=b_{i}/b_{\mathrm{p}} $$
式中： $ f_{p} $ ——加强板强度设计值（N/mm $ ^{2} $ ）；
$ C_{p} $ ——参数，按式(13.4.4-2)计算。
2) 对支管受压的 T、Y 和 X 形节点，当 $ \beta_{p} \leq 0.8 $ 时可应用下式进行加强板的设计。
$$ l_{\mathrm{p}}\geq2b\left/\sin\theta_{i}\right. $$
$$ t_{\mathrm{p}}\geq4t_{1}-t $$
3) 对 K 形间隙节点，可按本标准第 13.4.2 条中相应的公式计算承载力，这时用 $ t_{p} $ 代替 t，用加强板设计强度 $ f_{p} $ 代替主管设计强度 f。
2 对于侧板加强的 T、Y、X 和 K 形间隙方管节点（图 13.2.4(c)），可用本标准第 13.4.2 条中相应的计算主管侧壁承载力的公式计算，此时用 $ t + t_{p} $ 代替侧壁厚 t， $ A_{v} $ 取为 $ 2h(t + t_{p}) $ 。
13.4.5 方（矩）形管节点连接焊缝的计算应符合下列规定：
1 在节点处，支管沿周边与主管相焊，焊缝承载力不应小于节点承载力。
2 直接焊接的方（矩）形管节点中，轴心受力支管与主管的连接焊缝可视为全周角焊缝按下式计算：
$$ \frac{N_{i}}{h_{\mathrm{e}}l_{\mathrm{w}}}\leq f_{\mathrm{f}}^{\mathrm{w}} $$
式中： $ N_{i} $ ——支管轴力设计值（N）；
$ h_{e} $ ——角焊缝计算厚度，当支管承受轴力时，平均计算厚度可取 $ 0.7h_{r} $ （mm）；
$ l_{w} $ ——焊缝的计算长度，按本条第3款计算（mm）；
$ f_{f}^{w} $ ——角焊缝的强度设计值（N/mm $ ^{2} $ ）。
3 支管为方（矩）形管时，角焊缝的计算长度可按下列公式计算：
1）对于有间隙的 K 形和 N 形节点：
当 $ \theta_{i}\geq60^{\circ} $ 时：
$$ l_{\mathrm{w}}=\frac{2h_{i}}{\sin\theta_{i}}+b_{i} $$
当 $ \theta_{i}\leq50^{\circ} $ 时：
$$ l_{{w}}=\frac{2h{{i}}}{\sin\theta{{i}}}+2b{_{i}} $$
当 $ 50^{\circ}<\theta_{i}<60^{\circ} $ 时： $ l_{w} $ 按插值法确定。
2）对于 T、Y 和 X 形节点：
$$ l_{\mathrm{w}}=\frac{2h_{i}}{\sin\theta_{i}} $$
4 当支管为圆管时，焊缝计算长度应按下式计算：
$$ l_{\mathrm{w}}=\pi\big(a_{0}+b_{0}\big)-D_{i} $$
$$ a_{0}=\frac{R_{i}}{\sin\theta_{i}} $$
$$ b_{{0}}=R{_{i}} $$
式中： $ a_{0} $ ——椭圆相交线的长半轴（mm）；
$ b_{0} $ ——椭圆相交线的短半轴（mm）；
$ R_{i} $ ——圆支管半径（mm）；
$ \theta_{i} $ ——支管轴线与主管轴线的交角。