14 钢与混凝土组合梁
14 钢与混凝土组合梁
14.1 一般规定
14.1.1 本章规定适用于不直接承受动力荷载的组合梁。对于直接承受动力荷载的组合梁，应按本标准附录 J 的要求进行疲劳计算，其承载能力应按弹性方法进行计算。组合梁的翼板可采用现浇混凝土板、混凝土叠合板或压型钢板混凝土组合板等，其中混凝土板除应符合本章的规定外，尚应符合现行国家标准《混凝土结构设计规范》GB 50010 的有关规定。
14.1.2 在进行组合梁截面承载能力验算时，跨中及中间支座处混凝土翼板的有效宽度 $ b_{e} $ （图14.1.2）应按下式计算：
$$ b_{\mathrm{e}}=b_{0}+b_{1}+b_{2} $$
式中： $ b_{0} $ ——板托顶部的宽度：当板托倾角 $ \alpha<45^{\circ} $ 时，应按 $ \alpha=45^{\circ} $ 计算；当无板托时，则取钢梁上翼缘的宽度；当混凝土板和钢梁不直接接触（如之间有压型钢板分隔）时，取栓钉的横向间距，仅有一列栓钉时取 0（mm）；
$ b_{1} $ 、 $ b_{2} $ ——梁外侧和内侧的翼板计算宽度，当塑性中和轴位于混凝土板内时，各取梁等效跨径 $ l_{e} $ 的1/6。此外， $ b_{1} $ 尚不应超过翼板实际外伸宽度 $ S_{1} $ ； $ b_{2} $ 不应超过相邻钢梁上翼缘或板托间净距 $ S_{0} $ 的1/2（mm）；
$ l_{e} $ ——等效跨径。对于简支组合梁，取为简支组合梁的跨度。对于连续组合梁，中间跨正弯矩区取为0.6l，边跨正弯矩区取为0.8l，l为组合梁跨度，支座负弯矩区取为相邻两跨跨度之和的20%（mm）。
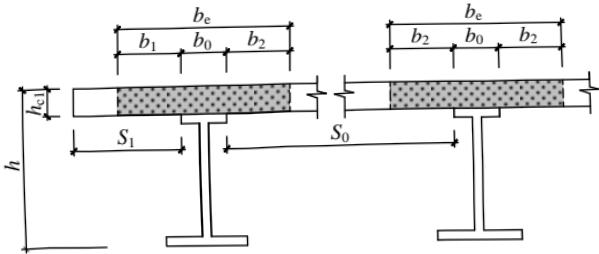
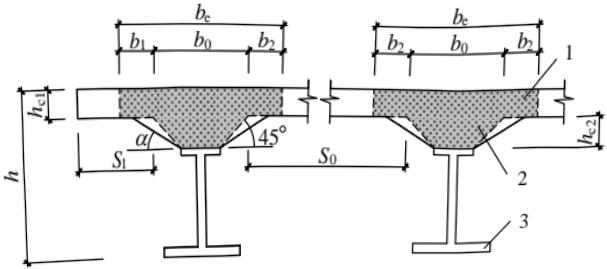
1—混凝土翼板；2—板托；3—钢梁
14.1.3 组合梁进行正常使用极限状态验算时应符合下列规定：
1 组合梁的挠度应按弹性方法进行计算，弯曲刚度宜按本标准第 14.4.2 条的规定计算。对于连续组合梁，在距中间支座两侧各 0.15l（l 为梁的跨度）范围内，不应计入受拉区混凝土对刚度的影响，但宜计入翼板有效宽度 $ b_{e} $ 范围内纵向钢筋的作用。
2 连续组合梁应按本标准第 14.5 节的规定验算负弯矩区段混凝土最大裂缝宽度。其负弯矩内力可按不考虑混凝土开裂的弹性分析方法计算并进行调幅。
3 对于露天环境下使用的组合梁以及直接受热源辐射作用的组合梁，应考虑温度效应的影响。钢梁和混凝土翼板间的计算温度差应按实际情况采用。
4 混凝土收缩产生的内力及变形可按组合梁混凝土板与钢梁之间的温差 $ -15^{\circ}C $ 计算。
5 考虑混凝土徐变影响时，可将钢与混凝土的弹性模量比放大一倍。
14.1.4 组合梁施工时，混凝土硬结前的材料重量和施工荷载应由钢梁承受，钢梁应根据实际临时支撑的情况按本标准第3章和第7章的规定验算其强度、稳定性和变形。
计算组合梁挠度和负弯矩区裂缝宽度时应考虑施工方法及工序的影响。计算组合梁挠度时，应将施工阶段的挠度和使用阶段续加荷载产生的挠度相叠加，当钢梁下有临时支撑时，应考虑拆除临时支撑时引起的附加变形。计算组合梁负弯矩区裂缝宽度时，可仅考虑形成组合截面后引入的支座负弯矩值。
14.1.5 在强度和变形满足要求时，组合梁可按部分抗剪连接进行设计。
14.1.6 按本章进行设计的组合梁，钢梁受压区的板件宽厚比应符合本标准第10章中塑性设计的相关规定。当组合梁受压上翼缘不符合塑性设计要求的板件宽厚比限值，但连接件满足下列要求时，仍可采用塑性方法进行设计：
1 当混凝土板沿全长和组合梁接触（如现浇楼板）时，连接件最大间距不大于 $ 22t_{f}\varepsilon_{k} $ ；当混凝土板和组合梁部分接触（如压型钢板横肋垂直于钢梁）时，连接件最大间距不大于
$ 15t_{f}\varepsilon_{k};\varepsilon_{k} $ 为钢号修正系数， $ t_{f} $ 为钢梁受压上翼缘厚度。
2 连接件的外侧边缘与钢梁翼缘边缘之间的距离不大于 $ 9t_{f}\varepsilon_{k} $ 。
14.1.7 组合梁承载能力按塑性分析方法进行计算时，连续组合梁和框架组合梁在竖向荷载作用下的内力可采用不考虑混凝土开裂的模型进行弹性分析，并按本标准第10章的规定对弯矩进行调幅，楼板的设计应符合现行国家标准《混凝土结构设计规范》GB50010的有关规定。
14.1.8 组合梁应按本标准第 14.6 节的规定进行混凝土翼板的纵向抗剪验算；在组合梁的强度、挠度和裂缝计算中，可不考虑板托截面。
14.2 组合梁设计
14.2.1 完全抗剪连接组合梁的受弯承载力应符合下列规定：
1 正弯矩作用区段：
1) 塑性中和轴在混凝土翼板内（图 14.2.1-1），即 $ Af \leq b_{e}h_{c1}f_{c} $ 时：
$$ M\leq b_{\mathrm{e}}xf_{\mathrm{c}}y $$
$$ x=A f/\left(b_{\mathrm{e}}f_{\mathrm{c}}\right) $$
式中：M——正弯矩设计值（N·mm）；
A——钢梁的截面面积（mm $ ^{2} $ ）；
x——混凝土翼板受压区高度（mm）；
y——钢梁截面应力的合力至混凝土受压区截面应力的合力间的距离（mm）；
$ f_{c} $ ——混凝土抗压强度设计值（N/mm $ ^{2} $ ）。
2）塑性中和轴在钢梁截面内（图14.2.1-2），即 $ Af>b_{c}h_{c1}f_{c} $ 时：
$$ M\leq b_{\mathrm{e}}h_{\mathrm{c}1}f_{\mathrm{c}}y_{1}+A_{\mathrm{c}}f y_{2} $$
$$ A_{\mathrm{c}}=0.5\left(A-b_{\mathrm{e}}h_{\mathrm{c1}}f_{\mathrm{c}}/f\right) $$
式中： $ A_{c} $ ——钢梁受压区截面面积（mm²）；
$ y_{1} $ ——钢梁受拉区截面形心至混凝土翼板受压区截面形心的距离（mm）；
$ y_{2} $ ——钢梁受拉区截面形心至钢梁受压区截面形心的距离（mm）。
2 负弯矩作用区段（图 14.2.1-3）：
$$ M^{\prime}\leq M_{\mathrm{s}}+A_{\mathrm{st}}f_{\mathrm{st}}\left(y_{3}+y_{4}/2\right) $$
$$ M_{\mathrm{s}}=\left(S_{1}+S_{2}\right)f $$
$$ f_{\mathrm{st}}A_{\mathrm{st}}+f\left(A-A_{\mathrm{c}}\right)=fA_{\mathrm{c}} $$
式中： $ M' $ ——负弯矩设计值（N·mm）；
$ S_{1} $ 、 $ S_{2} $ ——钢梁塑性中和轴（平分钢梁截面积的轴线）以上和以下截面对该轴的面积矩 $ \left(\mathrm{mm}^{3}\right) $ ;
$ A_{st} $ ——负弯矩区混凝土翼板有效宽度范围内的纵向钢筋截面面积（mm $ ^{2} $ ）；
$ f_{st} $ ——钢筋抗拉强度设计值（N/mm $ ^{2} $ ）:
$ y_{3} $ ——纵向钢筋截面形心至组合梁塑性中和轴的距离，根据截面轴力平衡式（14.2.1-7）求出钢梁受压区面积 $ A_{c} $ ，取钢梁拉压区交界处位置为组合梁塑性中和轴位置（mm）；
$ y_{4} $ ——组合梁塑性中和轴至钢梁塑性中和轴的距离。当组合梁塑性中和轴在钢梁腹板内时，取 $ y_{4}=A_{\mathrm{st}}f_{\mathrm{st}}/(2t_{\mathrm{w}}f) $ ，当该中和轴在钢梁翼缘内时，可取 $ y_{4} $ 等于钢梁塑性中和轴至腹板上边缘的距离（mm）。
1—组合截面塑性中和轴；2—钢梁截面塑性中和轴
14.2.2 部分抗剪连接组合梁在正弯矩区段的受弯承载力宜符合下列公式规定（图 14.2.2）：
$$ x=n_{\mathrm{r}}N_{\mathrm{v}}^{\mathrm{c}}/\left(b_{\mathrm{e}}f_{\mathrm{c}}\right) $$
$$ A_{\mathrm{c}}=\left(A f-n_{\mathrm{r}}N_{\mathrm{v}}^{\mathrm{c}}\right)\Big/(2f\Big) $$
$$ M_{\mathrm{u,r}}=n_{\mathrm{r}}N_{\mathrm{v}}^{\mathrm{c}}y_{\mathrm{l}}+0.5\left(Af-n_{\mathrm{r}}N_{\mathrm{v}}^{\mathrm{c}}\right)y_{2} $$
式中： $ M_{u,r} $ ——部分抗剪连接时组合梁截面正弯矩受弯承载力（N·mm）；
$ n_{r} $ ——部分抗剪连接时最大正弯矩验算截面到最近零弯矩点之间的抗剪连接件数目；
$ N_{v}^{c} $ ——每个抗剪连接件的纵向受剪承载力，按本标准第 14.3 节的有关公式计算（N）。
$ y_{1} $ 、 $ y_{2} $ ——如图 14.2.2 所示，可按式（14.2.2-2）所示的轴力平衡关系式确定受压钢梁的面积 $ A_{c} $ ，进而确定组合梁塑性中和轴的位置（mm）。
计算部分抗剪连接组合梁在负弯矩作用区段的受弯承载力时，仍按本标准式（14.2.1-5）计算，但 $ A_{st}f_{st} $ 应取 $ n_{t}N_{v}^{c} $ 和 $ A_{st}f_{st} $ 两者中的较小值， $ n_{r} $ 取为最大负弯矩验算截面到最近零弯矩点之间的抗剪连接件数目。
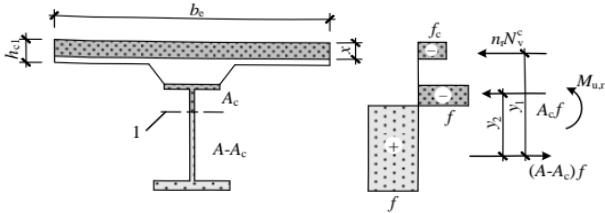
1—组合梁塑性中和轴
14.2.3 组合梁的受剪强度应按本标准式（10.3.2）计算。
14.2.4 用弯矩调幅设计法计算组合梁强度时，按下列规定考虑弯矩与剪力的相互影响：
1 受正弯矩的组合梁截面不考虑弯矩和剪力的相互影响；
2 受负弯矩的组合梁截面，当剪力设计值 $ V \leq 0.5 h_{w} t_{w} f_{v} $ 时，可不对验算负弯矩受弯承载力所用的腹板钢材强度设计值进行折减；当 $ V > 0.5 h_{w} t_{w} f_{v} $ 时，验算负弯矩受弯承载力所用的腹板钢材强度设计值 f 可折减为 $ (1 - \rho) f $ ，折减系数 $ \rho $ 应按下式计算：
$$ \rho=\left[2V/\left(h_{\mathrm{w}}t_{\mathrm{w}}f_{\mathrm{v}}\right)-1\right]^{2} $$
14.3 抗剪连接件的计算
14.3.1 组合梁的抗剪连接件宜采用圆柱头焊钉，也可采用槽钢或有可靠依据的其他类型连接件（图 14.3.1）。单个抗剪连接件的受剪承载力设计值应由下列公式确定：
1 圆柱头焊钉连接件：
$$ N_{\mathrm{v}}^{\mathrm{c}}=0.43A_{\mathrm{s}}\sqrt{E_{\mathrm{c}}f_{\mathrm{c}}}\leq0.7A_{\mathrm{s}}f_{\mathrm{u}} $$
式中： $ E_{c} $ ——混凝土的弹性模量（N/mm $ ^{2} $ ）；
$ A_{s} $ ——圆柱头焊钉钉杆截面面积（mm $ ^{2} $ ）；
$ f_{u} $ ——圆柱头焊钉极限抗拉强度设计值，需满足现行国家标准《电弧螺柱焊用圆柱头焊钉》GB/T 10433 的要求（N/mm²）。
2 槽钢连接件：
$$ N_{\mathrm{v}}^{\mathrm{c}}=0.26(t+0.5t_{\mathrm{w}})l_{\mathrm{c}}\sqrt{E_{\mathrm{c}}f_{\mathrm{c}}} $$
式中：t——槽钢翼缘的平均厚度（mm）；
$ t_{w} $ ——槽钢腹板的厚度（mm）；
$ l_{c} $ ——槽钢的长度（mm）。
槽钢连接件通过肢尖肢背两条通长角焊缝与钢梁连接，角焊缝按承受该连接件的受剪承载力设计值 $ N_{v}^{c} $ 进行计算。
14.3.2 对于用压型钢板混凝土组合板做翼板的组合梁（图 14.3.2），其焊钉连接件的受剪承载力设计值应分别按以下两种情况予以降低：
1 当压型钢板肋平行于钢梁布置（图 14.3.2（a））， $ b_{w}/h_{e}<1.5 $ 时，按本标准式（14.3.1-1）算得的 $ N_{v}^{c} $ 应乘以折减系数 $ \beta_{v} $ 后取用。 $ \beta_{v} $ 值按下式计算：
$$ \beta_{\mathrm{v}}=0.6\frac{b_{\mathrm{w}}}{h_{\mathrm{e}}}(\frac{h_{\mathrm{d}}-h_{\mathrm{e}}}{h_{\mathrm{e}}})\leq1 $$
式中： $ b_{w} $ ——混凝土凸肋的平均宽度，当肋的上部宽度小于下部宽度时（图 14.3.2（c）），改取上部宽度（mm）；
$ h_{e} $ ——混凝土凸肋高度（mm）；
$ h_{d} $ ——焊钉高度（mm）。
2 当压型钢板肋垂直于钢梁布置时（图 14.3.2（b）），焊钉连接件承载力设计值的折减系数按下式计算：
$$ \beta_{\mathrm{v}}=\frac{0.85}{\sqrt{n_{0}}}\frac{b_{\mathrm{w}}}{h_{\mathrm{e}}}(\frac{h_{\mathrm{d}}-h_{\mathrm{e}}}{h_{\mathrm{e}}})\leq1 $$
式中： $ n_{0} $ ——在梁某截面处一个肋中布置的焊钉数，当多于3个时，按3个计算。
14.3.3 位于负弯矩区段的抗剪连接件，其受剪承载力设计值 $ N_{v}^{c} $ 应乘以折减系数0.9。
14.3.4 当采用柔性抗剪连接件时，抗剪连接件的计算应以弯矩绝对值最大点及支座为界限，划分为若干个区段（图 14.3.4），逐段进行布置。每个剪跨区段内钢梁与混凝土翼板交界面的纵向剪力 $ V_{s} $ 应按下列公式确定：
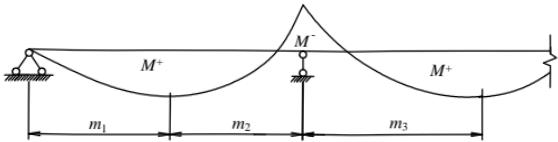
1 正弯矩最大点到边支座区段，即 $ m_{1} $ 区段， $ V_{s} $ 取 Af 和 $ b_{e}h_{c1}f_{c} $ 中的较小者。
2 正弯矩最大点到中支座（负弯矩最大点）区段，即 $ m_{2} $ 和 $ m_{3} $ 区段：
$$ V_{\mathrm{s}}=\min\left{A f,b_{\mathrm{e}}h_{\mathrm{c l}}f_{\mathrm{c}}\right}+A_{\mathrm{s t}}f_{\mathrm{s t}} $$
按完全抗剪连接设计时，每个剪跨区段内需要的连接件总数 $ n_{f} $ ，按下式计算：
$$ n_{\mathrm{f}}=V_{\mathrm{s}}/N_{\mathrm{v}}^{\mathrm{c}} $$
部分抗剪连接组合梁，其连接件的实配个数不得少于 $ n_{f} $ 的50%。
按式（14.3.4-2）算得的连接件数量，可在对应的剪跨区段内均匀布置。当在此剪跨区段内有较大集中荷载作用时，应将连接件个数 $ n_{f} $ 按剪力图面积比例分配后再各自均匀布置。
14.4 挠度计算
14.4.1 组合梁的挠度应分别按荷载的标准组合和准永久组合进行计算，以其中的较大值作为依据。挠度可按结构力学方法进行计算，仅受正弯矩作用的组合梁，其弯曲刚度应取考虑滑移效应的折减刚度，连续组合梁宜按变截面刚度梁进行计算。按荷载的标准组合和准永久组合进行计算时，组合梁应各取其相应的折减刚度。
14.4.2 组合梁考虑滑移效应的折减刚度 B 可按下式确定：
$$ B=\frac{EI_{eq}}{1+\xi} $$
式中：E——钢梁的弹性模量 $ (\mathrm{N}/\mathrm{mm}^{2}) $ ;
$ I_{eq} $ ——组合梁的换算截面惯性矩；对荷载的标准组合，可将截面中的混凝土翼板有效宽度除以钢与混凝土弹性模量的比值 $ \alpha_{E} $ 换算为钢截面宽度后，计算整个截面的惯性矩；对荷载的准永久组合，则除以 $ 2\alpha_{E} $ 进行换算；对于钢梁与压型钢板混凝土组合板构成的组合梁，应取其较弱截面的换算截面进行计算，且不计压型钢板的作用（mm $ ^{4} $ ）。
$ \xi $ ——刚度折减系数，宜按本标准第14.4.3条进行计算。
14.4.3 刚度折减系数 $ \xi $ 宜按下列公式计算（当 $ \xi \leqslant 0 $ 时，取 $ \xi = 0 $ ）：
$$ \xi=\eta\left[0.4-\frac{3}{\left(jl\right)^{2}}\right] $$
$$ \eta=\frac{36Ed_{c}pA_{0}}{n_{s}khl^{2}} $$
$$ j=0.81\sqrt{\frac{n_{\mathrm{s}}N_{\mathrm{v}}^{\mathrm{c}}A_{\mathrm{l}}}{EI_{0}p}}\ \left(\mathrm{mm^{-1}}\right) $$
$$ A_{0}=\frac{A_{\mathrm{cf}}A}{a_{\mathrm{E}}A+A_{\mathrm{cf}}} $$
$$ A_{1}=\frac{I_{0}+A_{0}d_{c}^{2}}{A_{0}} $$
$$ I_{0}=I+\frac{I_{\mathrm{cf}}}{\alpha_{\mathrm{E}}} $$
式中： $ A_{cr} $ ——混凝土翼板截面面积；对压型钢板混凝土组合板的翼板，应取其较弱截面的面积，且不考虑压型钢板（mm $ ^{2} $ ）；
A——钢梁截面面积（mm $ ^{2} $ ）；
I——钢梁截面惯性矩（mm $ ^{4} $ ）；
$ I_{cf} $ ——混凝土翼板的截面惯性矩；对压型钢板混凝土组合板的翼板，应取其较弱截面的惯性矩，且不考虑压型钢板（mm $ ^{4} $ ）；
$ d_{c} $ ——钢梁截面形心到混凝土翼板截面（对压型钢板混凝土组合板为其较弱截面）形心的距离（mm）；
h——组合梁截面高度（mm）；
l——组合梁的跨度（mm）；
$ N_{v}^{c} $ ——抗剪连接件的承载力设计值，应按本标准第 14.3.1 条的规定计算（单位取 N）；
p——抗剪连接件的纵向平均间距（mm）；
k——抗剪连接件刚度系数， $ k = N_{\mathrm{v}}^{\mathrm{c}} (\mathrm{N}/\mathrm{mm}) $ ;
$ n_{s} $ ——抗剪连接件在一根梁上的列数；
$ \alpha_{E} $ ——钢梁与混凝土弹性模量的比值。
14.5 负弯矩区裂缝宽度计算
14.5.1 组合梁负弯矩区段混凝土在正常使用极限状态下考虑长期作用影响的最大裂缝宽度 $ w_{max} $ 应按现行国家标准《混凝土结构设计规范》GB 50010 的规定按轴心受拉构件进行计算，其值不得大于现行国家标准《混凝土结构设计规范》GB 50010 所规定的限值。
14.5.2 按荷载效应的标准组合计算的开裂截面纵向受拉钢筋的应力 $ \sigma_{sk} $ 按下列公式计算：
$$ \sigma_{\mathrm{sk}}=\frac{M_{\mathrm{k}}y_{\mathrm{s}}}{I_{\mathrm{cr}}} $$
$$ M_{\mathrm{k}}=M_{\mathrm{e}}\left(1-\alpha_{\mathrm{r}}\right) $$
式中： $ I_{cr} $ ——由纵向普通钢筋与钢梁形成的组合截面的惯性矩（mm $ ^{4} $ ）；
$ y_{s} $ ——钢筋截面重心至钢筋和钢梁形成的组合截面中和轴的距离（mm）；
$ M_{k} $ ——钢与混凝土形成组合截面之后，考虑了弯矩调幅的标准荷载作用下支座截面负弯矩组合值，对于悬臂组合梁，式（14.5.2-2）中的 $ M_{k} $ 应根据平衡条件计算得到 $ (N \cdot mm) $ ;
$ M_{e} $ ——钢与混凝土形成组合截面之后，标准荷载作用下按未开裂模型进行弹性计算得到的连续组合梁中支座负弯矩值（N·mm）；
$ \alpha_{r} $ ——正常使用极限状态连续组合梁中支座负弯矩调幅系数，其取值不宜超过15%。
14.6 纵向抗剪计算
14.6.1 组合梁板托及翼缘板纵向受剪承载力验算时，应分别验算图 14.6.1 所示的纵向受剪界面 a-a、b-b、c-c 及 d-d。
$ A_{t} $ —混凝土板顶部附近单位长度内钢筋面积的总和（mm²/mm），包括混凝土板内抗弯和构造钢筋；
$ A_{b} $ 、 $ A_{bh} $ ——分别为混凝土板底部、承托底部单位长度内钢筋面积的总和（mm $ ^{2} $ /mm）。
14.6.2 单位纵向长度内受剪界面上的纵向剪力设计值应按下列公式计算：
1 单位纵向长度上 b-b、c-c 及 d-d 受剪界面（图 14.6.1）的计算纵向剪力为：
$$ v_{l,1}=\frac{V_{\mathrm{s}}}{m_{i}} $$
2 单位纵向长度上 a-a 受剪界面（图 14.6.1）的计算纵向剪力为：
$$ v_{l,1}=\max\left(\frac{V_{\mathrm{s}}}{m_{i}}\times\frac{b_{1}}{b_{\mathrm{e}}},\frac{V_{\mathrm{s}}}{m_{i}}\times\frac{b_{2}}{b_{\mathrm{e}}}\right) $$
式中： $ v_{l,1} $ ——单位纵向长度内受剪界面上的纵向剪力设计值；
$ V_{s} $ ——每个剪跨区段内钢梁与混凝土翼板交界面的纵向剪力，按本标准第 14.3.4 条的规定计算；
$ m_{i} $ ——剪跨区段长度（图 14.3.4）；
$ b_{1} $ 、 $ b_{2} $ ——分别为混凝土翼板左右两侧挑出的宽度（图 14.6.1）；
$ b_{e} $ ——混凝土翼板有效宽度，应按对应跨的跨中有效宽度取值，有效宽度应按本标准第14.1.2条的规定计算。
14.6.3 组合梁承托及翼缘板界面纵向受剪承载力计算应符合下列公式规定：
$$ v_{l,1}\leq v_{lu,1} $$
$$ v_{h a,1}=0.7f_{\mathrm{t}}b_{\mathrm{f}}+0.8A_{\mathrm{e}}f_{\mathrm{r}} $$
$$ v_{hu,1}=0.25b_{f}f_{c} $$
式中： $ v_{u,1} $ ——单位纵向长度内界面受剪承载力（N/mm），取式（14.6.3-2）和式（14.6.3-3）的较小值；
$ f_{t} $ ——混凝土抗拉强度设计值（N/mm $ ^{2} $ ）；
$ b_{f} $ ——受剪界面的横向长度，按图 14.6.1 所示的 a-a、b-b、c-c 及 d-d 连线在抗剪连接件以外的最短长度取值（mm）；
$ A_{e} $ ——单位长度上横向钢筋的截面面积 $ \left(\mathrm{mm}^{2}/\mathrm{mm}\right) $ ，按图14.6.1和表14.6.3取值；
$ f_{r} $ ——横向钢筋的强度设计值（N/mm $ ^{2} $ ）。
| 剪切面 | a-a | b-b | c-c | d-d |
| $ A_{e} $ | $ A_{b} + A_{t} $ | 2 $ A_{b} $ | 2 $ (A_{b} + A_{bh}) $ | 2 $ A_{bh} $ |
14.6.4 横向钢筋的最小配筋率应满足下式要求：
$$ A_{\mathrm{e}}f_{\mathrm{r}}/b_{\mathrm{f}}>0.75\left(\mathrm{N/mm^{2}}\right) $$
14.7 构造要求
14.7.1 组合梁截面高度不宜超过钢梁截面高度的 2 倍，混凝土板托高度 $ h_{c2} $ 不宜超过翼板厚度 $ h_{c1} $ 的 1.5 倍。
14.7.2 组合梁边梁混凝土翼板的构造应满足下列要求：
1 有板托时，伸出长度不宜小于 $ h_{c2} $ ;
2 无板托时，应同时满足伸出钢梁中心线不小于 150mm、伸出钢梁翼缘边不小于 50mm 的要求（图 14.7.2）。
14.7.3 连续组合梁在中间支座负弯矩区的上部纵向钢筋及分布钢筋，应按现行国家标准《混凝土结构设计规范》GB 50010 的规定设置。
14.7.4 抗剪连接件的设置应符合下列规定：
1 圆柱头焊钉连接件钉头下表面或槽钢连接件上翼缘下表面与翼板底部钢筋顶面的距离 $ h_{e0} $ 不宜小于 30mm;
2 连接件沿梁跨度方向的最大间距不应大于混凝土翼板（包括板托）厚度的3倍，且不大于300mm；连接件的外侧边缘与钢梁翼缘边缘之间的距离不应小于20mm；连接件的外侧边缘至混凝土翼板边缘间的距离不应小于100mm；连接件顶面的混凝土保护层厚度不应小于15mm。
14.7.5 圆柱头焊钉连接件除应满足本标准第 14.7.4 条的要求外，尚应符合下列规定：
1 当焊钉位置不正对钢梁腹板时，如钢梁上翼缘承受拉力，则焊钉钉杆直径不应大于钢梁上翼缘厚度的 1.5 倍；如钢梁上翼缘不承受拉力，则焊钉钉杆直径不应大于钢梁上翼缘厚度的 2.5 倍。
2 焊钉长度不应小于其杆径的 4 倍。
3 焊钉沿梁轴线方向的间距不应小于杆径的 6 倍，垂直于梁轴线方向的间距不应小于杆径的 4 倍。
4 用压型钢板作底模的组合梁，焊钉钉杆直径不宜大于 19mm，混凝土凸肋宽度不应小于焊钉钉杆直径的 2.5 倍；焊钉高度 $ h_{d} $ 应符合 $ h_{d} \geq h_{e} + 30 $ 的要求（本标准图 14.3.2）。
14.7.6 槽钢连接件一般采用 Q235 钢，截面不宜大于[12.6。
14.7.7 横向钢筋的构造要求应符合下列规定：
1 横向钢筋的间距不应大于 $ 4h_{e0} $ ，且不应大于 200mm。
2 板托中应配 U 形横向钢筋加强（本标准图 14.6.1）。板托中横向钢筋的下部水平段应该设置在距钢梁上翼缘 50mm 的范围以内。
14.7.8 对于承受负弯矩的箱形截面组合梁，可在钢箱梁底板上方或腹板内侧设置抗剪连接件并浇筑混凝土。