5 结构分析与稳定性设计
5 结构分析与稳定性设计
5.1 一般规定
5.1.1 建筑结构的内力和变形可按结构静力学方法进行弹性或弹塑性分析，采用弹性分析结果进行设计时，截面板件宽厚比等级为 S1、S2、S3 级的构件可有塑性变形发展。
5.1.2 结构稳定性设计应在结构分析或构件设计中考虑二阶效应。
5.1.3 结构的计算模型和基本假定应与构件连接的实际性能相符合。
5.1.4 框架结构的梁柱连接宜采用刚接或铰接。梁柱采用半刚性连接时，应计入梁柱交角变化的影响，在内力分析时，应假定连接的弯矩-转角曲线，并在节点设计时，保证节点的构造与假定的弯矩-转角曲线符合。
5.1.5 进行桁架杆件内力计算时应符合下列规定：
1 计算桁架杆件轴力时可采用节点铰接假定；
2 采用节点板连接的桁架腹杆及荷载作用于节点的弦杆，其杆件截面为单角钢、双角钢或 T 形钢时，可不考虑节点刚性引起的弯矩效应；
3 除无斜腹杆的空腹桁架外，直接相贯连接的钢管结构节点，当符合本标准第13章各类节点的几何参数适用范围且主管节间长度与截面高度或直径之比不小于12、支管杆间长度与截面高度或直径之比不小于24时，可视为铰接节点；
4 H形或箱形截面杆件的内力计算宜符合本标准第8.5节的规定。
5.1.6 结构内力分析可采用一阶弹性分析、二阶弹性分析或直接分析，应根据下列公式计算的最大二阶效应系数 $ \theta_{i,\max}^{II} $ 选用适当的结构分析方法。当 $ \theta_{i,\max}^{II} \leq 0.1 $ 时，可采用一阶弹性分析；当 $ 0.1 < \theta_{i,\max}^{II} \leq 0.25 $ 时，宜采用二阶弹性分析或采用直接分析；当 $ \theta_{i,\max}^{II} > 0.25 $ 时，宜增大结构的侧移刚度。
1 规则框架结构的二阶效应系数可按下式计算：
$$ \theta_{i}^{\mathrm{I I}}=\frac{\sum N_{\mathrm{k}i}\cdot\Delta u_{i}}{\sum H_{\mathrm{k}i}\cdot h_{i}} $$
式中： $ \sum N_{ki} $ ——所计算 i 楼层各柱轴心压力标准值之和（N）；
$ \sum H_{ki} $ ——产生层间侧移 $ \Delta u $ 的计算楼层及以上各层的水平力标准值之和（N）；
$ h_{i} $ ——所计算 i 楼层的层高（mm）；
$ \Delta u_{i} $ —— $ \sum H_{ki} $ 作用下按一阶弹性分析求得的计算楼层的层间侧移（mm）。
2 一般结构的二阶效应系数可按下式计算：
$$ \theta_{i}^{\mathrm{I I}}=\frac{1}{\eta_{\mathrm{e r}}} $$
式中： $ \eta_{cr} $ ——整体结构最低阶弹性临界荷载与荷载设计值的比值。
5.1.7 二阶 $ P-\Delta $ 弹性分析应考虑初始几何缺陷的影响，直接分析应考虑初始几何缺陷和残余应力的影响。
5.1.8 当对结构进行连续倒塌分析、抗火分析或在其他极端荷载作用下的结构分析时，可采用静力直接分析或动力直接分析。
5.1.9 以整体受压或受拉为主的大跨度钢结构的稳定性分析应采用二阶弹性分析或直接分析。
5.2 初始缺陷
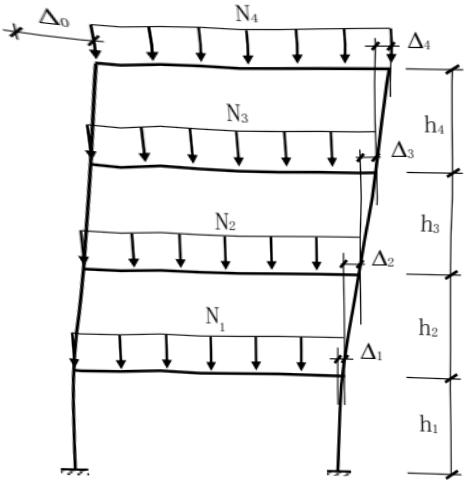
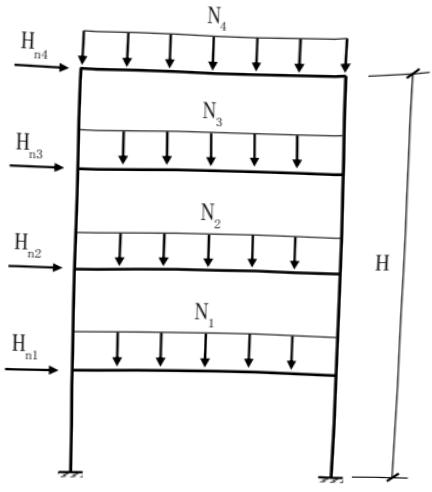
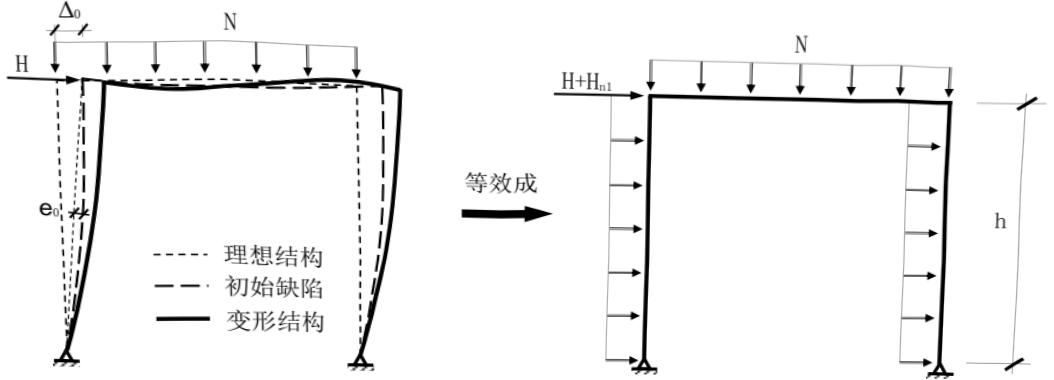
5.2.1 结构整体初始几何缺陷模式可按最低阶整体屈曲模态采用。框架及支撑结构整体初始几何缺陷代表值的最大值 $ \Delta_{0} $ （图 5.2.1）可取为 H/250，H 为结构总高度。框架及支撑结构整体初始几何缺陷代表值也可按式(5.2.1-1)确定（图 5.2.1-1）；或可通过在每层柱顶施加假想水平力 $ H_{ni} $ 等效考虑，假想水平力可按式（5.2.1-2）计算，施加方向应考虑荷载的最不利组合（图 5.2.1-2）。
$$ \Delta_{i}=\frac{h_{i}}{250}\sqrt{0.2+\frac{1}{n_{s}}} $$
$$ H_{\mathrm{n}i}=\frac{G_{i}}{250}\sqrt{0.2+\frac{1}{n_{\mathrm{s}}}} $$
式中： $ \Delta_{i} $ ——所计算 i 楼层的初始几何缺陷代表值（mm）；
$ n_{s} $ ——结构总层数，当 $ \sqrt{0.2+\frac{1}{n_{s}}}<\frac{2}{3} $ 时取此根号值为 $ \frac{2}{3} $ ；当 $ \sqrt{0.2+\frac{1}{n_{s}}}>1.0 $ 时，取此根号值为1.0；
$ h_{i} $ ——所计算楼层的高度（mm）；
$ G_{i} $ ——第i楼层的总重力荷载设计值（N）。
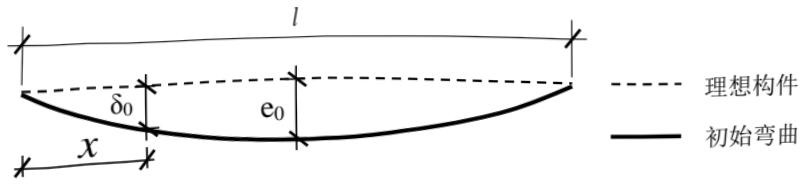
5.2.2 构件的初始缺陷代表值可按式(5.2.2-1)计算确定，该缺陷值包括了残余应力的影响
（图 5.2.2（a））。构件的初始缺陷也可采用假想均布荷载进行等效简化计算，假想均布荷载可按式（5.2.2-2）确定（图 5.2.2（b））。
$$ \delta_{\mathbf{0}}=e_{0}\sin\frac{\pi x}{l} $$
$$ q_{0}=\frac{8N_{\mathrm{k}}e_{0}}{l^{2}} $$
式中： $ \delta_{0} $ ——离构件端部x处的初始变形值（mm）；
$ e_{0} $ ——构件中点处的初始变形值（mm）；
x ——离构件端部的距离（mm）;
l——构件的总长度（mm）；
$ q_{0} $ ——等效分布荷载（N/mm）；
$ N_{k} $ ——构件承受的轴力标准值（N）。
构件初始弯曲缺陷值 $ \frac{e_{0}}{l} $ ，当采用直接分析不按弹塑性分析时，可按表5.2.2取构件综合缺陷代表值，当按本标准第5.5节采用直接分析按弹塑性分析时，应按本标准第5.5.8条或第5.5.9条考虑构件初始缺陷。
| 对应于表7.2.1-1和表7.2.1-2中的 柱子曲线 | 二阶分析采用的 $ \frac{e_0}{l} $ 值 |
| a类 | 1/400 |
| b类 | 1/350 |
| c类 | 1/300 |
| d类 | 1/250 |
5.3 一阶弹性分析与设计
5.3.1 钢结构的内力和位移计算采用一阶弹性分析时，应按本标准第6章~第8章的有关规定进行构件设计，应按本标准第11章、第12章的有关规定进行连接和节点设计。
5.3.2 对于形式和受力复杂的结构，当采用一阶弹性分析方法进行结构分析与设计时，应按结构弹性稳定理论确定构件的计算长度系数，并应按本标准第6章~第8章的有关规定进行构件设计。
5.4 二阶弹性 $ P-\Delta $ 分析与设计
5.4.1 采用仅考虑 $ P-\Delta $ 效应的二阶弹性分析时，应按本标准第 5.2.1 条考虑结构的整体初始缺陷，计算结构在各种荷载或作用设计值下的内力和标准值下位移，并应按本标准第 6 章~第 8 章的有关规定进行各结构构件的设计。计算构件轴心受压稳定承载力时，构件计算长度系数 $ \mu $ 可取 1.0 或其他认可的值。
5.4.2 二阶 $ P-\Delta $ 效应可按近似的二阶理论对一阶弯矩进行放大来考虑。对无支撑框架结构，杆件杆端的弯矩 $ M_{\Delta}^{II} $ 也可采用下列近似公式进行计算：
$$ M_{\Delta}^{\mathrm{I I}}=M_{\mathrm{q}}+\alpha_{i}^{\mathrm{I I}}M_{\mathrm{H}} $$
$$ \alpha_{i}^{\mathrm{I I}}=\frac{1}{1-\theta_{i}^{\mathrm{I I}}} $$
式中： $ M_{a} $ ——结构在竖向荷载作用下的一阶弹性弯矩（N·mm）；
$ M_{\Delta}^{II} $ ——仅考虑 $ P-\Delta $ 效应的二阶弯矩（N·mm）；
$ M_{H} $ ——结构在水平荷载作用下的一阶弹性弯矩（N·mm）；
$ \theta_{i}^{II} $ ——二阶效应系数，可按本标准第 5.1.6 条规定采用；
$ \alpha_{i}^{II} $ ——第 i 层杆件的弯矩增大系数；当 $ \alpha_{i}^{II}>1.33 $ 时，宜增大结构的侧移刚度。
5.5 直接分析设计法
5.5.1 直接分析设计法应采用考虑二阶 $ P-\Delta $ 和 $ P-\delta $ 效应，按本标准第 5.2.1 条、第 5.2.2 条、第 5.5.8 条和第 5.5.9 条同时考虑结构和构件的初始缺陷、节点连接刚度和其他对结构稳定性有显著影响的因素，允许材料的弹塑性发展和内力重分布，获得各种荷载设计值（作用）下
的内力和标准值（作用）下位移，同时在分析的所有阶段，各结构构件的设计均应符合本标准第6章~第8章的有关规定，但不需要按计算长度法进行构件受压稳定承载力验算。
5.5.2 直接分析法不按弹塑性分析时，结构分析应限于第一个塑性铰的形成，对应的荷载水平不应低于荷载设计值，不允许进行内力重分布。
5.5.3 直接分析法按弹塑性分析时宜采用塑性铰法或塑性区法。塑性铰形成的区域，构件和节点应有足够的延性保证以便内力重分布，允许一个或者多个塑性铰产生，构件的极限状态应根据设计目标及构件在整个结构中的作用来确定。
5.5.4 直接分析法按弹塑性分析时，钢材的应力-应变关系可为理想弹塑性，屈服强度可取本标准规定的强度设计值，弹性模量按本标准第4.4.8条采用。
5.5.5 直接分析法按弹塑性分析时，钢结构构件截面应为双轴对称截面或单轴对称截面，塑性铰处截面板件宽厚比等级应为 S1、S2 级，其出现的截面或区域应保证有足够的转动能力。
5.5.6 当结构采用直接分析设计法进行连续倒塌分析时，结构材料的应力-应变关系宜考虑应变率的影响；进行抗火分析时，应考虑结构材料在高温下的应力-应变关系对结构和构件内力产生的影响。
5.5.7 结构和构件采用直接分析设计法进行分析和设计时，计算结果可直接作为承载能力极限状态和正常使用极限状态下的设计依据，应按下列公式进行构件截面承载力验算：
1 当构件有足够侧向支撑以防止侧向失稳时：
$$ \frac{N}{Af}+\frac{M^{\mathrm{II}}{\mathrm{x}}}{M{\mathrm{cx}}}+\frac{M^{\mathrm{II}}{\mathrm{y}}}{M{\mathrm{cy}}}\leq1.0 $$
2 直接分析法不按弹塑性分析或按弹塑性分析但截面板件宽厚比等级不符合 S2 级要求时：
$$ M_{\mathrm{c x}}=\gamma_{\mathrm{x}}W_{\mathrm{x}}f $$
$$ M_{\mathrm{c y}}=\gamma_{\mathrm{y}}W_{\mathrm{y}}f $$
3 按弹塑性分析，截面板件宽厚比等级符合 S2 级要求时：
$$ M_{\mathrm{c x}}=W_{\mathrm{p x}}f $$
$$ M_{\mathrm{c y}}=W_{\mathrm{p y}}f $$
4 当构件可能产生侧向失稳时：
$$ \frac{N}{A f}+\frac{M_{\mathrm{x}}^{\mathrm{I I}}}{\varphi_{\mathrm{b}}W_{\mathrm{x}}f}+\frac{M_{\mathrm{y}}^{\mathrm{I I}}}{M_{\mathrm{c y}}}\leq1.0 $$
式中： $ M_{x}^{II} $ 、 $ M_{y}^{II} $ ——分别为绕 x 轴、y 轴的二阶弯矩设计值，可由结构分析直接得到
(N·mm);
A——构件的毛截面面积（mm $ ^{2} $ ）；
$ M_{cx} $ 、 $ M_{cy} $ ——分别为绕x轴、y轴的受弯承载力设计值（N·mm）；
$ W_{x} $ 、 $ W_{y} $ ——当构件板件宽厚比等级为S1级、S2级、S3级或S4级时，为构件绕x轴、y轴的毛截面模量；当构件板件宽厚比等级为S5级时，为构件绕x轴、y轴的有效截面模量（mm $ ^{3} $ ）；
$ W_{px} $ 、 $ W_{py} $ ——构件绕x轴、y轴的塑性毛截面模量（mm $ ^{3} $ ）；
$ \gamma_{x} $ 、 $ \gamma_{y} $ ——截面塑性发展系数，应按本标准第6.1.2条的规定采用；
$ \varphi_{b} $ ——梁的整体稳定系数，应按本标准附录 C 确定。
5.5.8 采用塑性铰法进行直接分析设计时，除应按本标准第 5.2.1 条、第 5.2.2 条考虑初始缺陷外，当受压构件所受轴力大于 0.5Af 时，其弯曲刚度应乘以刚度折减系数 0.8。
5.5.9 采用塑性区法进行直接分析设计时，应按不小于 1/1000 的出厂加工精度考虑构件的初始几何缺陷，并考虑初始残余应力。
5.5.10 大跨度钢结构体系的稳定性分析宜采用直接分析法。结构整体初始几何缺陷模式可按最低阶整体屈曲模态采用，最大缺陷值可取 L/300，L 为结构跨度。构件的初始缺陷可按本标准第 5.2.2 条的规定采用。