附录C 梁的整体稳定系数
附录 C 梁的整体稳定系数
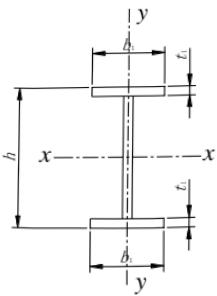
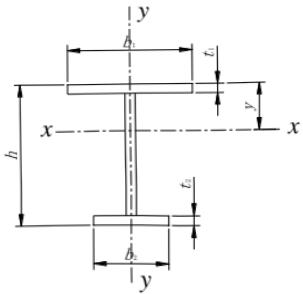
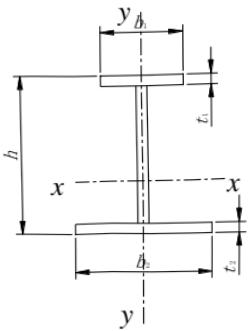
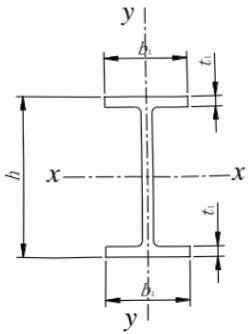
C.0.1 等截面焊接工字形和轧制 H 型钢（图 C.0.1）简支梁的整体稳定系数 $ \varphi_{b} $ 应按下列公式计算：
$$ \varphi_{\mathrm{b}}=\beta_{\mathrm{b}}\frac{4320}{\lambda_{\mathrm{y}}^{2}}\cdot\frac{A h}{W_{\mathrm{x}}}\left[\sqrt{1+\left(\frac{\lambda_{\mathrm{y}}t_{1}}{4.4h}\right)^{2}}+\eta_{\mathrm{b}}\right]\varepsilon_{\mathrm{k}} $$
$$ \lambda_{{y}}=\frac{l{{1}}}{i{_{y}}} $$
截面不对称影响系数 $ \eta_{h} $ 应按下列公式计算：
对双轴对称截面（(图 C.0.1 (a)、(d)):
$$ \eta_{\mathrm{b}}=0 $$
对单轴对称工字形截面（图 C.0.1（b）、（c））：
加强受压翼缘
$$ \eta_{\mathrm{b}}=0.8\big(2\alpha_{\mathrm{b}}-1\big) $$
加强受拉翼缘
$$ \eta_{\mathrm{b}}=2\alpha_{\mathrm{b}}-1 $$
$$ \alpha_{\mathrm{b}}=\frac{I_{1}}{I_{1}+I_{2}} $$
当按公式（C.0.1-1）算得的 $ \varphi_{b} $ 值大于0.6时，应用下式计算的 $ \varphi_{b}^{\prime} $ 代替 $ \varphi_{b} $ 值：
$$ \varphi^{\prime}{\mathrm{b}}=1.07-\frac{0.282}{\varphi{\mathrm{b}}}\leq1.0 $$
式中： $ \beta_{b} $ ——梁整体稳定的等效弯矩系数，应按表 C.0.1 采用；
$ \lambda_{v} $ ——梁在侧向支承点间对截面弱轴 y-y 的长细比；
A——梁的毛截面面积；
h、 $ t_{1} $ ——梁截面的全高和受压翼缘厚度，等截面铆接（或高强度螺栓连接）简支梁，其受压翼缘厚度 $ t_{1} $ 包括翼缘角钢厚度在内；
$ l_{1} $ ——梁受压翼缘侧向支承点之间的距离；
$ i_{y} $ ——梁毛截面对 y 轴的回转半径；
$ I_{1} $ 、 $ I_{2} $ ——分别为受压翼缘和受拉翼缘对 y 轴的惯性矩。
| 项次 | 侧向支承 | 荷载 | ξ≤2.0 | ξ>2.0 | 适用范围 | |
| 1 | 跨中无侧向支承 | 均布荷载作用在 | 上翼缘 | 0.69+0.13ξ | 0.95 | 图C.0.1(a)、(b)和(d)的截面 |
| 2 | 下翼缘 | 1.73-0.20ξ | 1.33 | |||
| 3 | 集中荷载作用在 | 上翼缘 | 0.73+0.18ξ | 1.09 | ||
| 4 | 下翼缘 | 2.23-0.28ξ | 1.67 | |||
| 5 | 跨度中点有一个侧向支承点 | 均布荷载作用在 | 上翼缘 | 1.15 | 图C.0.1中的所有截面 | |
| 6 | 下翼缘 | 1.40 | ||||
| 7 | 集中荷载作用在截面高度的任意位置 | 1.75 | ||||
| 8 | 跨中有不少于两个等距离侧向支承点 | 任意荷载作用在 | 上翼缘 | 1.20 | ||
| 9 | 下翼缘 | 1.40 | ||||
| 10 | 梁端有弯矩,但跨中无荷载作用 | 1.75-1.05(M2/M1)+0.3(M2/M1)2但≤2.3 | ||||
注：1 $ \xi $ 为参数， $ \xi=\frac{l_{1}t_{1}}{b_{1}h} $ ，其中 $ b_{1} $ 为受压翼缘的宽度。
2 $ M_{1} $ 和 $ M_{2} $ 为梁的端弯矩，使梁产生同向曲率时 $ M_{1} $ 和 $ M_{2} $ 取同号，产生反向曲率时取异号， $ \left|M_{1}\right|\geq\left|M_{2}\right| $ 。
3 表中项次 3、4 和 7 的集中荷载是指一个或少数几个集中荷载位于跨中央附近的情况，对其他情况的集中荷载，应按表中项次 1、2、5、6 内的数值采用。
4 表中项次 8、9 的 $ \beta_{b} $ ，当集中荷载作用在侧向支承点处时，取 $ \beta_{b}=1.20 $ 。
5 荷载作用在上翼缘系指荷载作用点在翼缘表面，方向指向截面形心；荷载作用在下翼缘系指荷载作用点在翼缘表面，方向背向截面形心。
6 对 $ \alpha_{b}>0.8 $ 的加强受压翼缘工字形截面，下列情况的 $ \beta_{b} $ 值应乘以相应的系数：
项次1：当 $ \xi\leq1.0 $ 时，乘以0.95；
项次3：当 $ \xi\leq0.5 $ 时，乘以0.90；当 $ 0.5<\xi\leq1.0 $ 时，乘以0.95。
C.0.2 轧制普通工字形简支梁的整体稳定系数 $ \varphi_{b} $ 应按表 C.0.2 采用，当所得的 $ \varphi_{b} $ 值大于 0.6 时，应按本标准式（C.0.1-7）算得的代替值。
| 项次 | 荷载情况 | 工字钢型号 | 自由长度l1（m） | ||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||
| 1 | 跨中无侧向支承点的梁 | 集中荷载作用于 | 上翼缘 | 10~20 | 2.00 | 1.30 | 0.99 | 0.80 | 0.68 | 0.58 | 0.53 | 0.48 | 0.43 |
| 22~32 | 2.40 | 1.48 | 1.09 | 0.86 | 0.72 | 0.62 | 0.54 | 0.49 | 0.45 | ||||
| 36~63 | 2.80 | 1.60 | 1.07 | 0.83 | 0.68 | 0.56 | 0.50 | 0.45 | 0.40 | ||||
| 2 | 下翼缘 | 10~20 | 3.10 | 1.95 | 1.34 | 1.01 | 0.82 | 0.69 | 0.63 | 0.57 | 0.52 | ||
| 22~40 | 5.50 | 2.80 | 1.84 | 1.37 | 1.07 | 0.86 | 0.73 | 0.64 | 0.56 | ||||
| 45~63 | 7.30 | 3.60 | 2.30 | 1.62 | 1.20 | 0.96 | 0.80 | 0.69 | 0.60 | ||||
| 3 | 均布荷载作用于 | 上翼缘 | 10~20 | 1.70 | 1.12 | 0.84 | 0.68 | 0.57 | 0.50 | 0.45 | 0.41 | 0.37 | |
| 22~40 | 2.10 | 1.30 | 0.93 | 0.73 | 0.60 | 0.51 | 0.45 | 0.40 | 0.36 | ||||
| 45~63 | 2.60 | 1.45 | 0.97 | 0.73 | 0.59 | 0.50 | 0.44 | 0.38 | 0.35 | ||||
| 4 | 下翼缘 | 10~20 | 2.50 | 1.55 | 1.08 | 0.83 | 0.68 | 0.56 | 0.52 | 0.47 | 0.42 | ||
| 22~40 | 4.00 | 2.20 | 1.45 | 1.10 | 0.85 | 0.70 | 0.60 | 0.52 | 0.46 | ||||
| 45~63 | 5.60 | 2.80 | 1.80 | 1.25 | 0.95 | 0.78 | 0.65 | 0.55 | 0.49 | ||||
| 5 | 跨中有侧向支承点的梁（不论荷载作用点在截面高度上的位置） | 10~20 | 2.20 | 1.39 | 1.01 | 0.79 | -0.66 | 0.57 | 0.52 | 0.47 | 0.42 | ||
| 22~40 | 3.00 | 1.80 | 1.24 | 0.96 | 0.76 | 0.65 | 0.56 | 0.49 | 0.43 | ||||
| 45~63 | 4.00 | 2.20 | 1.38 | 1.01 | 0.80 | 0.66 | 0.56 | 0.49 | 0.43 | ||||
注：1 同表 C.0.1 的注 3、5。
2 表中的 $ \varphi_{b} $ 适用于 Q235 钢。对其他钢号，表中数值应乘以 $ \varepsilon_{k} $ 。
C.0.3 轧制槽钢简支梁的整体稳定系数，不论荷载的形式和荷载作用点在截面高度上的位置，均可按下式计算：
$$ \varphi_{\mathrm{b}}=\frac{570b t}{l_{\mathrm{l}}h}\cdot\varepsilon_{\mathrm{k}}^{2} $$
式中：h、b、t——分别为槽钢截面的高度、翼缘宽度和平均厚度。
当按公式（C.0.3）算得的 $ \varphi_{b} $ 值大于 0.6 时，应按本标准式（C.0.1-7）算得相应的 $ \varphi_{b}^{\prime} $ 代替 $ \varphi_{b} $ 值。
C.0.4 双轴对称工字形等截面悬臂梁的整体稳定系数，可按本标准式（C.0.1-1）计算，但式中系数 $ \beta_{b} $ 应按表 C.0.4 查得，当按本标准式（C.0.1-2）计算长细比 $ \lambda_{y} $ 时， $ l_{1} $ 为悬臂梁的悬伸长度。当求得的 $ \varphi_{b} $ 值大于 0.6 时，应按本标准式（C.0.1-7）算得的 $ \varphi_{b}^{\prime} $ 代替 $ \varphi_{b} $ 值。
| 项次 | 荷载形式 | 0.60≤ξ≤1.24 | 1.24<ξ≤1.96 | 1.96<ξ≤3.10 | |
| 1 | 自由端一个集中荷载作用在 | 上翼缘 | 0.21+0.67ξ | 0.72+0.26ξ | 1.17+0.03ξ |
| 2 | 下翼缘 | 2.94-0.65ξ | 2.64-0.40ξ | 2.15-0.15ξ | |
| 3 | 均布荷载作用在上翼缘 | 0.62+0.82ξ | 1.25+0.31ξ | 1.66+0.10ξ | |
注：1 本表是按支承端为固定的情况确定的，当用于由邻跨延伸出来的伸臂梁时，应在构造上采取措施加强支承处的抗扭能力。
2 表中 $ \xi $ 见表 C.0.1 注 1。
C.0.5 均匀弯曲的受弯构件，当 $ \lambda_{y} \leq 120\varepsilon_{k} $ 时，其整体稳定系数 $ \varphi_{b} $ 可按下列近似公式计算：
1 工字形截面：
双轴对称
$$ \varphi_{\mathrm{b}}=1.07-\frac{\lambda_{\mathrm{y}}^{2}}{44000\varepsilon_{\mathrm{k}}^{2}} $$
单轴对称
$$ \varphi_{\mathrm{b}}=1.07-\frac{W_{\mathrm{x}}}{\left(2\alpha_{\mathrm{b}}+0.1\right)A h}\cdot\frac{\lambda_{\mathrm{y}}^{2}}{14000\varepsilon_{\mathrm{k}}^{2}} $$
2 弯矩作用在对称轴平面，绕 x 轴的 T 形截面：
1) 弯矩使翼缘受压时：
双角钢 T 形截面
$$ \varphi_{\mathrm{b}}=1-0.0017\lambda_{\mathrm{y}}/\varepsilon_{\mathrm{k}} $$
剖分 T 型钢和两板组合 T 形截面
$$ \varphi_{\mathrm{b}}=1-0.0022\lambda_{\mathrm{y}}/\varepsilon_{\mathrm{k}} $$
2) 弯矩使翼缘受拉且腹板宽厚比不大于 $ 18 \varepsilon_{k} $ 时：
$$ \varphi_{\mathrm{b}}=1-0.0005\lambda_{\mathrm{y}}/\varepsilon_{\mathrm{k}} $$
当按公式（C.0.5-1）和公式（C.0.5-2）算得的 $ \varphi_{b} $ 值大于1.0时，取 $ \varphi_{b}=1.0 $ 。