附录 E 柱的计算长度系数

附录 E 柱的计算长度系数

E.0.1 无侧移框架柱的计算长度系数 $ \mu $ 应按表 E.0.1 取值，同时符合下列规定：

1 当横梁与柱铰接时，取横梁线刚度为零。

2 对低层框架柱，当柱与基础铰接时，应取 $ K_{2}=0 $ ，当柱与基础刚接时，应取 $ K_{2}=10 $ ，平板支座可取 $ K_{2}=0.1 $ 。

3 当与柱刚接的横梁所受轴心压力 $ N_{b} $ 较大时，横梁线刚度折减系数 $ \alpha_{N} $ 应按下列公式计算：

横梁远端与柱刚接和横梁远端与柱铰接时：

$$ \alpha_{\mathrm{N}}=1-N_{\mathrm{b}}/N_{\mathrm{E b}} $$

横梁远端嵌固时：

$$ \alpha_{\mathrm{N}}=1-N_{\mathrm{b}}/\left(2N_{\mathrm{E b}}\right) $$

$$ N_{\mathrm{E b}}=\pi^{2}E I_{\mathrm{b}}/l^{2} $$

式中： $ I_{b} $ ——横梁截面惯性矩（mm $ ^{4} $ ）；

l——横梁长度（mm）。

表 E.0.1 无侧移框架柱的计算长度系数 $ \mu $

Kt	0	0.05	0.1	0.2	0.3	0.4	0.5	1	2	3	4	5	≥10
0	1.000	0.990	0.981	0.964	0.949	0.935	0.922	0.875	0.820	0.791	0.773	0.760	0.732
0.05	0.990	0.981	0.971	0.955	0.940	0.926	0.914	0.867	0.814	0.784	0.766	0.754	0.726
0.1	0.981	0.971	0.962	0.946	0.931	0.918	0.906	0.860	0.807	0.778	0.760	0.748	0.721
0.2	0.964	0.955	0.946	0.930	0.916	0.903	0.891	0.846	0.795	0.767	0.749	0.737	0.711
0.3	0.949	0.940	0.931	0.916	0.902	0.889	0.878	0.834	0.784	0.756	0.739	0.726	0.701
0.4	0.935	0.926	0.918	0.903	0.889	0.877	0.866	0.823	0.774	0.747	0.730	0.719	0.693
0.5	0.922	0.914	0.906	0.891	0.878	0.866	0.855	0.813	0.765	0.738	0.721	0.710	0.685
1	0.875	0.867	0.860	0.846	0.834	0.823	0.813	0.774	0.729	0.704	0.688	0.677	0.654
2	0.820	0.814	0.807	0.795	0.784	0.774	0.765	0.729	0.686	0.663	0.648	0.638	0.615
3	0.791	0.784	0.778	0.767	0.756	0.747	0.738	0.704	0.663	0.640	0.625	0.616	0.593
4	0.773	0.766	0.760	0.749	0.739	0.730	0.721	0.688	0.648	0.625	0.611	0.601	0.580
5	0.760	0.754	0.748	0.737	0.728	0.719	0.710	0.677	0.638	0.616	0.601	0.592	0.570
≥10	0.732	0.726	0.721	0.711	0.701	0.693	0.685	0.654	0.615	0.593	0.580	0.570	0.549

注：1 表中的计算长度系数 $ \mu $ 值系按下式算得：

$$ \left[\left(\frac{\pi}{\mu}\right)^{2}+2(K_{1}+K_{2})-4K_{1}K_{2}\right]\frac{\pi}{\mu}\cdot\sin\frac{\pi}{\mu}-2\left[(K_{1}+K_{2})\left(\frac{\pi}{\mu}\right)^{2}+4K_{1}K_{2}\right]\cos\frac{\pi}{\mu}+8K_{1}K_{2}=0 $$

式中， $ K_{1}, K_{2} $ 分别为相交子柱上端、柱下端的横梁线刚度之和与柱线刚度之和的比值。当梁远端为铰接时，应将横梁线刚度乘以1.5；当横梁远端为嵌固时，则将横梁线刚度乘以2。

E.0.2 有侧移框架柱的计算长度系数 $ \mu $ 应按表 E.0.2 取值，同时符合下列规定：

1 当横梁与柱铰接时，取横梁线刚度为零。

2 对低层框架柱，当柱与基础铰接时，应取 $ K_{2}=0 $ ，当柱与基础刚接时，应取 $ K_{2}=10 $ ，平板支座可取 $ K_{2}=0.1 $ 。

3 当与柱刚接的横梁所受轴心压力 $ N_{b} $ 较大时，横梁线刚度折减系数 $ \alpha_{N} $ 应按下列公式计算：

横梁远端与柱刚接时：

$$ \alpha_{\mathrm{N}}=1-N_{\mathrm{b}}/\left(4N_{\mathrm{E b}}\right) $$

横梁远端与柱铰接时：

$$ \alpha_{\mathrm{N}}=1-N_{\mathrm{b}}/N_{\mathrm{E b}} $$

横梁远端嵌固时：

$$ \alpha_{\mathrm{N}}=1-N_{\mathrm{b}}/\left(2N_{\mathrm{E b}}\right) $$

表 E.0.2 有侧移框架柱的计算长度系数 $ \mu $

K1K2	0	0.05	0.1	0.2	0.3	0.4	0.5	1	2	3	4	5	≥10
0	∞	6.02	4.45	3.42	3.01	2.78	2.64	2.33	2.17	2.11	2.08	2.07	2.03
0.05	6.02	4.16	3.47	2.86	2.58	2.42	2.31	2.07	1.94	1.90	1.87	1.86	1.83
0.1	4.46	3.47	3.01	2.56	2.33	2.20	2.11	1.90	1.79	1.75	1.73	1.72	1.70
0.2	3.42	2.86	2.36	2.23	2.05	1.94	1.87	1.70	1.60	1.57	1.55	1.54	1.52
0.3	3.01	2.58	2.33	2.05	1.90	1.80	1.74	1.58	1.49	1.46	1.45	1.44	1.42
0.4	2.78	2.42	2.20	1.94	1.80	1.71	1.65	1.50	1.42	1.39	1.37	1.37	1.35
0.5	2.64	2.31	2.11	1.87	1.74	1.65	1.59	1.45	1.37	1.34	1.32	1.32	1.30
1	2.33	2.07	1.90	1.70	1.58	1.50	1.45	1.32	1.24	1.21	1.20	1.19	1.17
2	2.17	1.94	1.79	1.60	1.49	1.42	1.37	1.24	1.16	1.14	1.12	1.12	1.10
3	2.11	1.90	1.75	1.57	1.46	1.39	1.34	1.21	1.14	1.11	1.10	1.09	1.07
4	2.08	1.87	1.73	1.55	1.45	1.37	1.32	1.20	1.12	1.10	1.08	1.08	1.06
5	2.07	1.86	1.72	1.54	1.44	1.37	1.32	1.19	1.12	1.09	1.08	1.07	1.05
≥10	2.03	1.83	1.70	1.52	1.42	1.35	1.30	1.17	1.10	1.07	1.06	1.05	1.03

注：1 表中的计算长度系数 $ \mu $ 值系按下式算得：

$$ \left[\frac{36K_{1}K_{2}-\left(\frac{\pi}{\mu}\right)^{2}}{}\right]\sin\frac{\pi}{\mu}+6(K_{1}+K_{2})\frac{\pi}{\mu}\cdot\cos\frac{\pi}{\mu}=0 $$

式中， $ K_{1}, K_{2} $ 分别为相交于柱上端、柱下端的横梁线刚度之和与柱线刚度之和的比值。当横梁远端为铰接时，应将横梁线刚度乘以0.5；当横梁远端为嵌固时，则应乘以2/3。

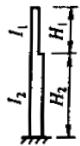
E.0.3 柱上端为自由的单阶柱下段的计算长度系数 $ \mu_{2} $ 应按表 E.0.3 取值。

表 E.0.3 柱上端为自由的单阶柱下段的计算长度系数 $ \mu_{2} $

简图	K1	0.06	0.08	0.10	0.12	0.14	0.16	0.18	0.20	0.22	0.24	0.26	0.28	0.3	0.4	0.5	0.6	0.7	0.8
	0.2	2.00	2.01	2.01	2.01	2.01	2.01	2.01	2.02	2.02	2.02	2.02	2.02	2.02	2.03	2.04	2.05	2.06	2.07
	0.3	2.01	2.02	2.02	2.02	2.03	2.03	2.03	2.04	2.04	2.05	2.05	2.05	2.06	2.08	2.10	2.12	2.13	2.15
	0.4	2.02	2.03	2.04	2.04	2.05	2.06	2.07	2.07	2.08	2.09	2.09	2.10	2.11	2.14	2.18	2.21	2.25	2.28
	0.5	2.04	2.05	2.06	2.07	2.09	2.10	2.11	2.12	2.13	2.15	2.16	2.17	2.18	2.24	2.29	2.35	2.40	2.45
K1=I1/I2·H2/H1	0.6	2.06	2.08	2.10	2.12	2.14	2.16	2.18	2.19	2.21	2.23	2.25	2.26	2.28	2.36	2.44	2.52	2.59	2.66
	0.7	2.10	2.13	2.16	2.18	2.21	2.24	2.26	2.29	2.31	2.34	2.36	2.38	2.41	2.52	2.62	2.72	2.81	2.90
	0.8	2.15	2.20	2.24	2.27	2.31	2.34	2.38	2.41	2.44	2.47	2.50	2.53	2.56	2.70	2.82	2.94	3.06	3.16
	0.9	2.24	2.29	2.35	2.39	2.44	2.48	2.52	2.56	2.60	2.63	2.67	2.71	2.74	2.90	3.05	3.19	3.32	3.44
	1.0	2.36	2.43	2.48	2.54	2.59	2.64	2.69	2.73	2.77	2.82	2.86	2.90	2.94	3.12	3.29	3.45	3.59	3.74
η1=H1/H2√(N1/N2·I2/I1)	1.2	2.69	2.76	2.83	2.89	2.95	3.01	3.07	3.12	3.17	3.22	3.27	3.32	3.37	3.59	3.80	3.99	4.17	4.34
	1.4	3.07	3.14	3.22	3.29	3.36	3.42	3.48	3.55	3.61	3.66	3.72	3.78	3.83	4.09	4.33	4.56	4.77	4.97
	1.6	3.47	3.55	3.63	3.71	3.78	3.85	3.92	3.99	4.07	4.12	4.18	4.25	4.31	4.61	4.88	5.14	5.38	5.62
N1——上段柱的轴心力；	1.8	3.88	3.97	4.05	4.13	4.21	4.29	4.37	4.44	4.52	4.59	4.66	4.73	4.80	5.13	5.44	5.73	6.00	6.26
N2——下段柱的轴心力	2.0	4.29	4.39	4.48	4.57	4.65	4.74	4.82	4.90	4.99	5.07	5.14	5.22	5.30	5.66	6.00	6.32	6.63	6.92
	2.2	4.71	4.81	4.91	5.00	5.10	5.19	5.28	5.37	5.46	5.54	5.63	5.71	5.80	6.19	6.57	6.92	7.26	7.58
	2.4	5.13	5.24	5.34	5.44	5.54	5.64	5.74	5.84	5.93	6.03	6.12	6.21	6.30	6.73	7.14	7.52	7.89	8.24
	2.6	5.55	5.66	5.77	5.88	5.99	6.10	6.20	6.31	6.41	6.51	6.61	6.71	6.80	7.27	7.71	8.13	8.52	8.90
	2.8	5.97	6.09	6.21	6.33	6.44	6.55	6.67	6.78	6.89	6.99	7.10	7.21	7.31	7.81	8.28	8.73	9.16	9.57
	3.0	6.39	6.52	6.64	6.77	6.89	7.01	7.13	7.25	7.37	7.48	7.59	7.71	7.82	8.35	8.86	9.34	9.80	10.24

注：表中的计算长度系数 $ \mu_{2} $ 值系按下式计算得出：

$$ \eta_{1}K_{1}\cdot\operatorname{tg}\frac{\pi}{\mu_{2}}\cdot\operatorname{tg}\frac{\pi\eta_{1}}{\mu_{2}}-1=0 $$

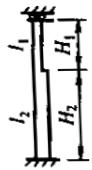
E.0.4 柱上端可移动但不转动的单阶柱下段的计算长度系数 $ \mu_{2} $ 应按表 E.0.4 取值。

表 E.0.4 柱上端可移动但不转动的单阶柱下段的计算长度系数 $ \mu_{2} $

简图	K1	η1	0.06	0.08	0.10	0.12	0.14	0.16	0.18	0.20	0.22	0.24	0.26	0.28	0.3	0.4	0.5	0.6	0.7	0.8
	0.2	1.96	1.94	1.93	1.91	1.90	1.89	1.88	1.86	1.85	1.84	1.83	1.82	1.81	1.76	1.72	1.68	1.65	1.62
	0.3	1.96	1.94	1.93	1.92	1.91	1.89	1.88	1.87	1.86	1.85	1.84	1.83	1.82	1.77	1.73	1.70	1.66	1.63
	0.4	1.96	1.95	1.94	1.92	1.91	1.90	1.89	1.88	1.87	1.86	1.85	1.84	1.83	1.79	1.75	1.72	1.68	1.66
	0.5	1.96	1.95	1.94	1.93	1.92	1.91	1.90	1.89	1.88	1.87	1.86	1.85	1.85	1.81	1.77	1.74	1.71	1.69
	0.6	1.97	1.96	1.95	1.94	1.93	1.92	1.91	1.90	1.90	1.89	1.88	1.87	1.87	1.83	1.80	1.78	1.75	1.73
	0.7	1.97	1.97	1.96	1.95	1.94	1.94	1.93	1.92	1.92	1.91	1.90	1.90	1.89	1.86	1.84	1.82	1.80	1.78
	0.8	1.98	1.98	1.97	1.96	1.96	1.95	1.95	1.94	1.94	1.93	1.93	1.93	1.92	1.90	1.88	1.87	1.86	1.84
	0.9	1.99	1.99	1.98	1.98	1.98	1.97	1.97	1.97	1.97	1.96	1.96	1.96	1.96	1.95	1.94	1.93	1.92	1.92
	1.0	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00	2.00
K1=I1/I2·H2/H1	1.2	2.03	2.04	2.04	2.05	2.06	2.07	2.07	2.08	2.08	2.09	2.10	2.10	2.11	2.13	2.15	2.17	2.18	2.20
	1.4	2.07	2.09	2.11	2.12	2.14	2.16	2.17	2.18	2.20	2.21	2.22	2.23	2.24	2.29	2.33	2.37	2.40	2.42
η1=H1/H2√N1/N2·I2/I1	1.6	2.13	2.16	2.19	2.22	2.25	2.27	2.30	2.32	2.34	2.36	2.37	2.39	2.41	2.48	2.54	2.59	2.63	2.67
	1.8	2.22	2.27	2.31	2.35	2.39	2.42	2.45	2.48	2.50	2.53	2.55	2.57	2.59	2.69	2.76	2.83	2.88	2.93
N1——上段柱的轴心力；	2.0	2.35	2.41	2.46	2.50	2.55	2.59	2.62	2.66	2.69	2.72	2.75	2.77	2.80	2.91	3.00	3.08	3.14	3.20
N2——下段柱的轴心力	2.2	2.51	2.57	2.63	2.68	2.73	2.77	2.81	2.85	2.89	2.92	2.95	2.98	3.01	3.14	3.25	3.33	3.41	3.47
	2.4	2.68	2.75	2.81	2.87	2.92	2.97	3.01	3.05	3.09	3.13	3.17	3.20	3.24	3.38	3.50	3.59	3.68	3.75
	2.6	2.87	2.94	3.00	3.06	3.12	3.17	3.22	3.27	3.31	3.35	3.39	3.43	3.46	3.62	3.75	3.86	3.95	4.03
	2.8	3.06	3.14	3.20	3.27	3.33	3.38	3.43	3.48	3.53	3.58	3.62	3.66	3.70	3.87	4.01	4.13	4.23	4.32
	3.0	3.26	3.34	3.41	3.47	3.54	3.60	3.65	3.70	3.75	3.80	3.85	3.89	3.93	4.12	4.27	4.40	4.51	4.61

注：表中的计算长度系数 $ \mu_{2} $ 值系按下式计算得出：

$$ \mathrm{tg}\frac{\pi\eta_{1}}{\mu_{2}}+\eta_{1}K_{1}\cdot\mathrm{tg}\frac{\pi}{\mu_{2}}=0 $$

柱上端为自由的双阶柱下段的计算长度系数 $ \mu_{3} $ 应按下列公式计算，也可按表 E.0.5 取值。

表 E.0.5 柱上端为自由的双阶柱下段的计算长度系数 $ \mu_{3} $

简图

K1

简图

K1

注：表中的计算长度系数 $ \mu_{s} $ 值系按下式算得：

$$ \frac{\eta_{1}K_{1}}{\eta_{2}K_{2}}\cdot\frac{\pi\eta_{1}}{\mu_{1}}\cdot\frac{\pi\eta_{2}}{\mu_{2}}+\frac{\pi\eta_{1}}{\eta_{1}}K_{1}\cdot\frac{\pi\eta_{1}}{\mu_{1}}\cdot\frac{\pi\eta_{2}}{\mu_{2}}+\frac{\pi\eta_{1}}{\eta_{2}}K_{2}\cdot\frac{\pi\eta_{2}}{\mu_{2}}\cdot\frac{\pi\eta_{1}}{\mu_{1}}-1=0 $$

表 E.0.6 柱顶可移动但不转动的双阶柱下段的计算长度系数 $ \mu_{3} $

简图

K1

简图

R1

注：表中的计算长度系数 $ \mu_{r} $ 值系按下式算得：

$$ \frac{\pi_{1}K_{1}}{\pi_{2}K_{2}}\cdot\operatorname{ctg}\frac{\pi\eta_{1}}{\mu_{3}}\cdot\operatorname{ctg}\frac{\pi\eta_{2}}{\mu_{3}}+\frac{\pi_{1}K_{1}}{(\pi_{2}K_{2})^{2}}\cdot\operatorname{ctg}\frac{\pi\eta_{2}}{\mu_{3}}\cdot\operatorname{ctg}\frac{\pi\eta_{3}}{\mu_{3}}+\frac{1}{\pi_{2}K_{2}}\cdot\operatorname{ctg}\frac{\pi\eta_{2}}{\mu_{3}}\cdot\operatorname{ctg}\frac{\pi\eta_{3}}{\mu_{3}}-1=0 $$