附录 F 加劲钢板剪力墙的弹性屈曲临界应力
F.1 仅设置竖向加劲的钢板剪力墙
F.1.1 仅设置竖向加劲的钢板剪力墙，其弹性剪切屈曲临界应力 $ \tau_{cr} $ 计算应符合下列规定：
1 参数 $ \eta_{y} $ 、 $ \eta_{rth} $ 应按下列公式计算：
$$ \eta_{y}=\frac{EI_{sy}}{Da_{1}} $$
$$ \eta_{\mathrm{r t h}}=6\eta_{\mathrm{k}}\left(7\beta^{2}-5\right)\geq10 $$
$$ \eta_{\mathrm{k}}=0.42+\frac{0.58}{\left[1+5.42\left(I_{\mathrm{t,sy}}/I_{\mathrm{sy}}\right)^{2.6}\right]^{0.77}} $$
$$ 0.8\leq\beta=\frac{H_{\mathrm{n}}}{a_{1}}\leq5 $$
式中：E——加劲肋的弹性模量 $ (\mathrm{N}/\mathrm{mm}^{2}) $ ;
$ I_{sy} $ ——竖向加劲肋的惯性矩 $ \left(\mathrm{mm}^{4}\right) $ ，可考虑加劲肋与钢板剪力墙有效宽度组合截面，单侧钢板剪力墙的有效宽度取15倍的钢板厚度；
D——单位宽度的弯曲刚度（N·mm），根据本标准式（9.2.4-3）计算；
$ a_{1} $ ——剪力墙板区格宽度（mm）;
$ H_{n} $ ——钢板剪力墙的净高度（mm）；
$ I_{t,sv} $ ——竖向加劲肋自由扭转常数（mm $ ^{4} $ ）。
2 当 $ \eta_{v}\geq\eta_{th} $ 时，弹性剪切屈曲临界应力 $ \tau_{cr} $ 应按下列公式计算：
$$ \tau_{\mathrm{cr}}=\tau_{\mathrm{crp}}=k_{\mathrm{rp}}\frac{\pi^{2}D}{a_{1}^{2}t_{\mathrm{w}}} $$
$$ k_{\mathrm{r p}}=\chi\left[5.34+\frac{4}{\left(H_{\mathrm{n}}/a_{1}\right)^{2}}\right] $$
当 $ \frac{H_{n}}{a_{1}}<1 $ 时：
$$ k_{\mathrm{r p}}=\chi\left[4+\frac{5.34}{\left(a_{\mathrm{l}}/H_{\mathrm{n}}\right)^{2}}\right] $$
式中： $ t_{w} $ ——剪力墙板的厚度（mm）；
$ \chi $ ——采用闭口加劲肋时取1.23，开口加劲肋时取1.0。
3 当 $ \eta_{y} < \eta_{th} $ 时，弹性剪切屈曲临界应力 $ \tau_{cr} $ 应按下列公式计算：
$$ \tau_{\mathrm{cr}}=k_{\mathrm{ss}}\frac{\pi^{2}D}{a_{1}^{2}t_{\mathrm{w}}} $$
$$ k_{\mathrm{s s}}=k_{\mathrm{s s0}}\left(\frac{a_{\mathrm{l}}}{L_{\mathrm{n}}}\right)^{2}+\left[k_{\tau\mathrm{p}}-k_{\mathrm{s s0}}\left(\frac{a_{\mathrm{l}}}{L_{\mathrm{n}}}\right)^{2}\right]\left(\frac{\eta_{\mathrm{y}}}{\eta_{\tau\mathrm{t h}}}\right)^{0.6} $$
当 $ \frac{H_{n}}{L_{n}}\geq1 $ 时：
$$ k_{\mathrm{ss0}}=6.5+\frac{5}{\left(H_{\mathrm{n}}/L_{\mathrm{n}}\right)^{2}} $$
当 $ \frac{H_{n}}{L_{n}}<1 $ 时：
$$ k_{\mathrm{ss0}}=5+\frac{6.5}{\left(L_{\mathrm{n}}/H_{\mathrm{n}}\right)^{2}} $$
式中： $ L_{n} $ ——钢板剪力墙的净宽度（mm）。
F.1.2 仅设置竖向加劲肋的钢板剪力墙，其竖向受压弹性屈曲临界应力 $ \sigma_{cr} $ 的计算应符合下列规定：
1 参数 $ \eta_{\sigma th} $ 应按下列公式计算：
$$ \eta_{\sigma\mathrm{th}}=1.5\left(1+\frac{1}{n_{\mathrm{v}}}\right)\left[k_{\mathrm{pan}}\left(n_{\mathrm{v}}+1\right)^{2}-k_{\sigma0}\right]\left(\frac{H_{\mathrm{n}}}{L_{\mathrm{n}}}\right)^{2} $$
$$ k_{\sigma0}=\chi\left(\frac{L_{\mathrm{n}}}{H_{\mathrm{n}}}+\frac{H_{\mathrm{n}}}{L_{\mathrm{n}}}\right)^{2} $$
式中： $ k_{pan} $ ——小区格竖向受压屈曲系数，可以取 $ k_{pan}=4\chi $ ， $ \chi $ 是嵌固系数，取1.23；
$ n_{v} $ ——竖向加劲肋的道数。
2 竖向受压弹性屈曲临界应力 $ \sigma_{cr} $ 应按下列公式计算：
当 $ \eta_{y}\geq\eta_{\sigma th} $ 时：
$$ \sigma_{\mathrm{cr}}=\sigma_{\mathrm{crp}}=k_{\mathrm{pan}}\frac{\pi^{2}D}{a_{1}^{2}t_{\mathrm{w}}} $$
当 $ \eta_{y}<\eta_{\sigma th} $ 时：
$$ \sigma_{\mathrm{cr}}=\sigma_{\mathrm{cr0}}+\left(\sigma_{\mathrm{crp}}-\sigma_{\mathrm{cr0}}\right)\frac{\eta_{\mathrm{y}}}{\eta_{\sigma\mathrm{th}}} $$
$$ \sigma_{\mathrm{cr0}}=\frac{\pi^{2}k_{\sigma0}D}{L_{\mathrm{n}}^{2}t_{\mathrm{w}}} $$
式中： $ k_{\sigma0} $ ——参数，按本标准式（F.1.2-2）计算。
F.1.3 仅设置竖向加劲肋的钢板剪力墙，其竖向抗弯弹性屈曲临界应力 $ \sigma_{bcr} $ 应按下列公式计算：
当 $ \eta_{y}\geq\eta_{\sigma th} $ 时：
$$ \sigma_{\mathrm{bcr}}=\sigma_{\mathrm{bcrp}}=k_{\mathrm{bpan}}\frac{\pi^{2}D}{a_{1}^{2}t_{\mathrm{w}}} $$
$$ k_{\mathrm{b p a n}}=4+2\beta_{\sigma}+2\beta_{\sigma}^{3} $$
当 $ \eta_{y}<\eta_{\sigma th} $ 时：
$$ \sigma_{\mathrm{bcr}}=\sigma_{\mathrm{bcr0}}+\left(\sigma_{\mathrm{bcrp}}-\sigma_{\mathrm{bcr0}}\right)\frac{\eta_{\mathrm{y}}}{\eta_{\mathrm{oth}}} $$
$$ \sigma_{\mathrm{bcr0}}=\frac{\pi^{2}k_{\mathrm{b0}}D}{L_{\mathrm{n}}^{2}t_{\mathrm{w}}} $$
$$ k_{\mathrm{b}0}=14+11\Bigg(\frac{H_{\mathrm{n}}}{L_{\mathrm{n}}}\Bigg)^{2}+2.2\Bigg(\frac{L_{\mathrm{n}}}{H_{\mathrm{n}}}\Bigg)^{2} $$
式中： $ k_{bpan} $ ——小区格竖向不均匀受压屈曲系数；
$ \beta_{\sigma} $ ——区格两边的应力差除以较大的压应力。
F.2 设置水平加劲的钢板剪力墙
F.2.1 仅设置水平加劲的钢板剪力墙，其弹性剪切屈曲临界应力 $ \tau_{cr} $ 计算应符合下列规定：
1 参数 $ \eta_{x} $ 、 $ \eta_{th,h} $ 应按下列公式计算：
$$ \eta_{x}=\frac{EI_{sx}}{Dh_{1}} $$
$$ \eta_{\tau\mathrm{t h,h}}=6\eta_{\mathrm{h}}\left(7\beta_{h}^{2}-4\right)\geq5 $$
$$ \eta_{\mathrm{h}}=0.42+\frac{0.58}{\left[1+5.42\left(I_{\mathrm{t,sx}}/I_{\mathrm{s}x}\right)^{2.6}\right]^{0.77}} $$
$$ 0.8\leq\beta_{h}=\frac{L_{n}}{h_{1}}\leq5 $$
式中： $ I_{sx} $ ——水平方向加劲肋的惯性矩（mm $ ^{4} $ ），可考虑加劲肋与钢板剪力墙有效宽度组合截面，单侧钢板剪力墙的有效宽度取15倍的钢板厚度；
$ h_{1} $ ——剪力墙板区格高度（mm）；
$$ I_{tsx}——水平加劲肋自由扭转常数（mm^{4}） $$
2 当 $ \eta_{x}\geq\eta_{thh} $ 时，弹性剪切屈曲临界应力 $ \tau_{cr} $ 应按下列公式计算：
$$ \tau_{\mathrm{cr}}=\tau_{\mathrm{crp}}=k_{\mathrm{rp}}\frac{\pi^{2}D}{L_{\mathrm{n}}^{2}t_{\mathrm{w}}} $$
$$ \frac{h_{1}}{L_{n}}\geq1 $$
$$ k_{rp}=\chi\left[5.34+\frac{4}{\left(h_{1}/L_{n}\right)^{2}}\right] $$
当 $ \frac{h_{1}}{L_{n}}<1 $ 时：
$$ k_{rp}=\chi\Bigg[4+\frac{5.34}{\left(L_{n}/h_{1}\right)^{2}}\Bigg] $$
3 当 $ \eta_{x}<\eta_{th,h} $ 时，弹性剪切屈曲临界应力 $ \tau_{cr} $ 应按下列公式计算：
$$ \tau_{\mathrm{cr}}=k_{\mathrm{ss}}\frac{\pi^{2}D}{L_{\mathrm{n}}^{2}t_{\mathrm{w}}} $$
$$ k_{\mathrm{s s}}=k_{\mathrm{s s0}}+\Big[k_{\tau\mathrm{p}}-k_{\mathrm{s s0}}\Big]\Bigg(\frac{\eta_{\mathrm{x}}}{\eta_{\tau\mathrm{t h,h}}}\Bigg)^{0.6} $$
式中： $ k_{ss0} $ ——参数，根据本标准式（F.1.1-10）、（F.1.1-11）计算。
F.2.2 仅设置水平加劲肋的钢板剪力墙，其竖向受压弹性屈曲临界应力 $ \sigma_{cr} $ 的计算应符合下列规定：
1 参数 $ \eta_{x0} $ 应按下式计算：
$$ \eta_{\mathrm{x}0}=0.3\Bigg(1+\cos\frac{\pi}{n_{\mathrm{h}}+1}\Bigg)\Bigg[1+\Bigg(\frac{L_{\mathrm{n}}}{h_{1}}\Bigg)^{2}\Bigg]^{2} $$
式中： $ n_{h} $ ——水平加劲肋的道数。
2 竖向受压弹性屈曲临界应力 $ \sigma_{cr} $ 应按下列公式计算：
当 $ \eta_{x}\geq\eta_{x0} $ 时
$$ \sigma_{\mathrm{cr}}=\sigma_{\mathrm{crp}}=k_{\mathrm{pan}}\frac{\pi^{2}D}{L_{\mathrm{n}}^{2}t_{\mathrm{w}}} $$
$$ k_{\mathrm{p a n}}=\left(\frac{L_{\mathrm{n}}}{h_{1}}+\frac{h_{1}}{L_{\mathrm{n}}}\right)^{2} $$
当 $ \eta_{x}<\eta_{x0} $ 时：
$$ \sigma_{\mathrm{c r}}=\sigma_{\mathrm{c r0}}+\Big(\sigma_{\mathrm{c r p}}-\sigma_{\mathrm{c r0}}\Big)\Bigg(\frac{\eta_{\mathrm{y}}}{\eta_{\mathrm{o t h}}}\Bigg)^{0.6} $$
式中： $ \sigma_{cr0} $ ——未加劲钢板剪力墙的竖向弯曲屈曲应力（N/mm $ ^{2} $ ），按本标准式（F.1.2-5）计算。
F.2.3 仅设置水平加劲肋的钢板剪力墙，其竖向抗弯弹性屈曲临界应力 $ \sigma_{bcr} $ 应按下列公式计算：
当 $ \eta_{x}\geq\eta_{x0} $ 时：
$$ \sigma_{\mathrm{bcr}}=\sigma_{\mathrm{bcrp}}=k_{\mathrm{bpan}}\frac{\pi^{2}D}{L_{\mathrm{n}}^{2}t_{\mathrm{w}}} $$
$$ k_{\mathrm{b p a n}}=14+11\Bigg(\frac{h_{\mathrm{l}}}{L_{\mathrm{n}}}\Bigg)^{2}+2.2\Bigg(\frac{L_{\mathrm{n}}}{h_{\mathrm{l}}}\Bigg)^{2} $$
当 $ \eta_{x}<\eta_{x0} $ 时：
$$ \sigma_{\mathrm{bcr}}=\sigma_{\mathrm{bcr0}}+\left(\sigma_{\mathrm{bcrp}}-\sigma_{\mathrm{bcr0}}\right)\left(\frac{\eta_{\mathrm{y}}}{\eta_{\mathrm{\sigma th}}}\right)^{0.6} $$
式中： $ \sigma_{bcr0} $ ——未加劲钢板剪力墙的竖向弯曲屈曲应力（N/mm $ ^{2} $ ），按本标准式（F.1.3-4）计算。
F.3 同时设置水平和竖向加劲肋的钢板剪力墙
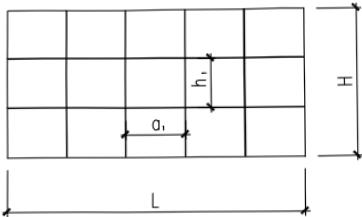
F.3.1 同时设置水平和竖向加劲肋的钢板剪力墙（图 F.3.1），其弹性剪切屈曲临界应力 $ \tau_{cr} $ 的计算应符合下列规定：
1 当加劲肋的刚度满足本标准第9.2.4条的要求时，其弹性剪切屈曲临界应力 $ \tau_{cr} $ 应按下列公式计算：
$$ \tau_{\mathrm{cr}}=\tau_{\mathrm{crp}}=k_{\mathrm{ss}}^{1}\frac{\pi^{2}D}{a_{1}^{2}t_{\mathrm{w}}} $$
当 $ \frac{a_{1}}{h_{1}}\geq1 $ 时
$$ k_{\mathrm{ss}}^{1}=6.5+\frac{5}{\left(h_{1}/a_{1}\right)^{2}} $$
当 $ \frac{a_{1}}{h_{1}}<1 $ 时
$$ k_{\mathrm{ss}}^{1}=5+\frac{6.5}{\left(a_{1}/h_{1}\right)^{2}} $$
2 当加劲肋的刚度不满足本标准第 9.2.4 条的要求时，其弹性剪切屈曲临界应力 $ \tau_{cr} $ 应按下列公式计算：
$$ \tau_{\mathrm{cr}}=\tau_{\mathrm{cr0}}+\Big(\tau_{\mathrm{crp}}-\tau_{\mathrm{cr0}}\Big)\Bigg(\frac{\eta_{\mathrm{av}}}{33}\Bigg)^{0.7}\leq\tau_{\mathrm{crp}} $$
$$ \tau_{\mathrm{cr0}}=k_{\mathrm{ss0}}\frac{\pi^{2}D}{L_{\mathrm{n}}^{2}t_{\mathrm{w}}} $$
$$ \eta_{av}=\sqrt{0.66\frac{EI_{sx}}{Da_{1}}\cdot\frac{EI_{sy}}{Dh_{1}}} $$
式中： $ \tau_{crp} $ ——小区格的剪切屈曲临界应力（N/mm $ ^{2} $ ）；
$ \tau_{cr0} $ ——未加劲板的剪切屈曲临界应力（N/mm $ ^{2} $ ）。
F.3.2 同时设置水平和竖向加劲肋的钢板剪力墙，其竖向受压弹性屈曲临界应力 $ \sigma_{cr} $ 的计算应符合下列规定：
1 当加劲肋的刚度满足本标准第9.2.4条的要求时，其竖向受压弹性屈曲临界应力 $ \sigma_{cr} $ 应按下列公式计算：
$$ \sigma_{\mathrm{c r}}=k_{\sigma0}^{1}\frac{\pi^{2}D}{a_{1}^{2}t_{\mathrm{w}}} $$
$$ k_{\sigma0}^{1}=\chi\left(\frac{a_{1}}{h_{1}}+\frac{h_{1}}{a_{1}}\right)^{2} $$
2 当加劲肋的刚度不满足本标准第9.2.4条的要求时，其竖向受压弹性屈曲临界应力 $ \sigma_{\alpha} $ 的计算应符合下列规定：
1）参数 $ D_{x} $ 、 $ D_{y} $ 、 $ D_{xy} $ 应按下列公式计算：
$$ D_{\mathrm{x}}=D+\frac{EI_{\mathrm{sx}}}{h_{1}} $$
$$ D_{\mathrm{y}}=D+\frac{EI_{\mathrm{sy}}}{a_{\mathrm{l}}} $$
$$ D_{\mathrm{xy}}=D+\frac{1}{2}\Bigg[\frac{GI_{\mathrm{t,sx}}}{a_{1}}+\frac{GI_{\mathrm{t,sy}}}{h_{1}}\Bigg] $$
式中：G——加劲肋的剪变模量 $ (\mathrm{N}/\mathrm{mm}^{2}) $ 。
2）竖向临界应力应按下列公式计算：
当 $ \frac{H_{n}}{L_{n}}\leq\left(\frac{D_{x}}{D_{y}}\right)^{0.25} $ 时：
$$ \sigma_{\mathrm{cr}}=\frac{\pi^{2}}{L_{\mathrm{n}}^{2}t_{\mathrm{w}}}\left[\left(\frac{H_{\mathrm{n}}}{L_{\mathrm{n}}}\right)^{2}D_{\mathrm{x}}+\left(\frac{L_{\mathrm{n}}}{H_{\mathrm{n}}}\right)^{2}D_{\mathrm{y}}+2D_{\mathrm{xy}}\right] $$
当 $ \frac{H_{n}}{L_{n}}>\left(\frac{D_{x}}{D_{y}}\right)^{0.25} $ 时：
$$ \sigma_{\mathrm{cr}}=\frac{2\pi^{2}}{L_{\mathrm{n}}^{2}t_{\mathrm{w}}}\Big[\sqrt{D_{\mathrm{x}}D_{\mathrm{y}}}+D_{\mathrm{xy}}\Big] $$
F.3.3 同时设置水平和竖向加劲肋的钢板剪力墙，其竖向抗弯弹性屈曲临界应力 $ \sigma_{bcr} $ 应按下列公式计算：
当 $ \frac{H_{n}}{L_{n}}\leq\frac{2}{3}\left(\frac{D_{x}}{D_{y}}\right)^{0.25} $ 时：
$$ \sigma_{\mathrm{bcr}}=\frac{6\pi^{2}}{L_{\mathrm{n}}^{2}t_{\mathrm{w}}}\left[\left(\frac{H_{\mathrm{n}}}{L_{\mathrm{n}}}\right)^{2}D_{\mathrm{x}}+\left(\frac{L_{\mathrm{n}}}{H_{\mathrm{n}}}\right)^{2}D_{\mathrm{y}}+2D_{\mathrm{xy}}\right] $$
当 $ \frac{H_{n}}{L_{n}}>\frac{2}{3}\left(\frac{D_{x}}{D_{y}}\right)^{0.25} $ 时：
$$ \sigma_{\mathrm{bcr}}=\frac{12\pi^{2}}{L_{\mathrm{n}}^{2}t_{w}}\Big[\sqrt{D_{\mathrm{x}}D_{\mathrm{y}}}+D_{\mathrm{xy}}\Big] $$