7 轴心受力构件
7 轴心受力构件¶
7.1 截面强度计算¶
7.1.1¶
轴心受拉构件,当端部连接及中部拼接处组成截面的各板件都有连接件直接传力时,其截面强度计算应符合下列规定:
1 除采用高强度螺栓摩擦型连接者外,其截面强度应采用下列公式计算:毛截面屈服:
$$ \sigma=\frac{N}{A}\leq f \tag{7.1.1-1} $$
净截面断裂:
$$ \sigma=\frac{N}{A_{n}}\leq0.7f_{u} \tag{7.1.1-2} $$
2 采用高强度螺栓摩擦型连接的构件,其截面强度计算应符合下列规定:
1)当构件为沿全长都有排列较密螺栓的组合构件时,其截面强度应按下式计算:
$$ \frac{N}{A_{n}}\leq f \tag{7.1.1-3} $$
2)除第1)项的情况外,其毛截面强度计算应采用式(7.1.1-1),净截面断裂应按下式计算:
$$ \sigma=(1-0.5\frac{n_{\mathrm{l}}}{n})\frac{N}{A_{\mathrm{n}}}\leq0.7f_{\mathrm{u}} \tag{7.1.1-4} $$
式中:N ——所计算截面处的拉力设计值(N);
f ——钢材的抗拉强度设计值(N/mm²);
A——构件的毛截面面积(mm $ ^{2} $ );
$ A_{n} $ ——构件的净截面面积,当构件多个截面有孔时,取最不利的截面 $ \left(\mathrm{mm}^{2}\right) $ ;
$ f_{u} $ ——钢材的抗拉强度最小值(N/mm $ ^{2} $ );
n——在节点或拼接处,构件一端连接的高强度螺栓数目;
$ n_{1} $ ——所计算截面(最外列螺栓处)上高强度螺栓数目。
7.1.2¶
轴心受压构件,当端部连接及中部拼接处组成截面的各板件都有连接件直接传力时,截面强度应按本标准式(7.1.1-1)计算。但含有虚孔的构件尚需在孔心所在截面按本标准式(7.1.1-2)计算。
7.1.3¶
轴心受拉构件和轴心受压构件,当其组成板件在节点或拼接处并非全部直接传力时,应对危险截面的面积乘以有效截面系数 $ \eta $ ,不同构件截面形式和连接方式的 $ \eta $ 值应符合表 7.1.3 的规定。
| 构件截面形式 | 连接形式 | $ \eta $ | 图例 |
| 角钢 | 单边连接 | 0.85 | 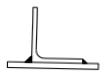 |
| 工字形、H形 | 翼缘连接 | 0.90 | 工字形、H形 |
| 腹板连接 | 0.70 | 腹板连接 |
7.2 轴心受压构件的稳定性计算¶
7.2.1¶
除可考虑屈服后强度的实腹式构件外,轴心受压构件的稳定性计算应符合下式要求:
$$ \frac{N}{\varphi A f}\leq1.0 \tag{7.2.1-1} $$
式中: $ \varphi $ ——轴心受压构件的稳定系数(取截面两主轴稳定系数中的较小者),根据构件的长细比(或换算长细比)、钢材屈服强度和表7.2.1-1、表7.2.1-2的截面分类,按本标准附录D采用。
| 截面形式 | 对x轴 | 对y轴 | |
 轧制 轧制 | a类 | a类 | |
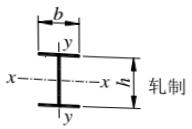 | b/h≤0.8 | a类 | b类 |
| b/h>0.8 | a*类 | b*类 | |
 轧制等边角钢 轧制等边角钢 | a*类 | a*类 | |
 焊接、翼缘为焰切边 焊接、翼缘为焰切边 | 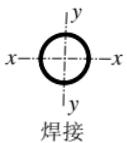 | b类 | b类 |
 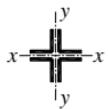 | |||
 轧制、焊接(板件宽厚比>20) 轧制、焊接(板件宽厚比>20) |  轧制或焊接 轧制或焊接 | ||
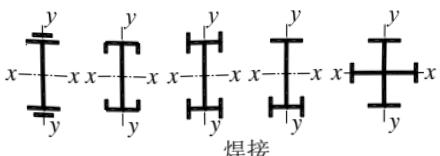 |  轧制截面和翼缘为焰切边的焊接截面 轧制截面和翼缘为焰切边的焊接截面 | ||
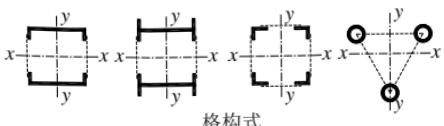 |  焊接,板件边缘焰切 焊接,板件边缘焰切 | ||
 焊接,翼缘为轧制或剪切边 焊接,翼缘为轧制或剪切边 | b类 | c类 | |
 焊接,板件边缘轧制或剪切 焊接,板件边缘轧制或剪切 |  轧制、焊接(板件宽厚比≤20) 轧制、焊接(板件宽厚比≤20) | c类 | c类 |
注:1 a类含义为 Q235 钢取 b 类,Q345、Q390、Q420 和 Q460 钢取 a 类;b类含义为 Q235 钢取 c 类,Q345、Q390、Q420 和 Q460 钢取 b 类。
2 无对称轴且剪心和形心不重合的截面,其截面分类可按有对称轴的类似截面确定,如不等边角钢采用等边角钢的类别;当无类似截面时,可取 c 类。
| 截面形式 | 对x轴 | 对y轴 | |
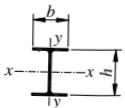 | t<80mm | b类 | c类 |
| 轧制工字形或H形截面 | t≥80mm | c类 | d类 |
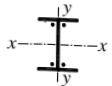 | 翼缘为焰切边 | b类 | b类 |
| 焊接工字形截面 | 翼缘为轧制或剪切边 | c类 | d类 |
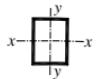 | 板件宽厚比>20 | b类 | b类 |
| 焊接箱形截面 | 板件宽厚比≤20 | c类 | c类 |
7.2.2¶
实腹式构件的长细比 $ \lambda $ 应根据其失稳模式,由下列公式确定:
1 截面形心与剪心重合的构件:
1)当计算弯曲屈曲时,长细比按下列公式计算:
$$ \lambda_{{x}}=\frac{l $$}}{i_{x}} \tag{7.2.2-1
$$ \lambda_{\mathrm{y}}=\frac{l_{\mathrm{0y}}}{i_{\mathrm{y}}} \tag{7.2.2-2} $$
式中: $ l_{0x} $ 、 $ l_{0y} $ ——分别为构件对截面主轴x和y的计算长度,根据本标准第7.4节的规定采用(mm);
$ i_{x} $ 、 $ i_{y} $ ——分别为构件截面对主轴x和y的回转半径(mm)。
2)当计算扭转屈曲时,长细比应按下式计算,双轴对称十字形截面板件宽厚比不超过 $ 15\varepsilon_{k} $ 者,可不计算扭转屈曲。
$$ \lambda_{z}=\sqrt{\frac{I_{0}}{I_{\mathrm{t}}/25.7+I_{\omega}/l_{\omega}^{2}}} \tag{7.2.2-3} $$
式中: $ I_{0} $ 、 $ I_{t} $ 、 $ I_{\omega} $ ——分别为构件毛截面对剪心的极惯性矩(mm $ ^{4} $ )、自由扭转常数(mm $ ^{4} $ )和
扇性惯性矩 $ \left(\mathrm{mm}^{6}\right) $ ,对十字形截面可近似取 $ I_{\omega}=0 $ ;
$ l_{\omega} $ ——扭转屈曲的计算长度,两端铰支且端截面可自由翘曲者,取几何长度l;
两端嵌固且端部截面的翘曲完全受到约束者,取0.5l(mm)。
2 截面为单轴对称的构件:
1) 计算绕非对称主轴的弯曲屈曲时,长细比应由式(7.2.2-1)、式(7.2.2-2)计算确定。计算绕对称主轴的弯扭屈曲时,长细比应按下式计算确定:
$$ \lambda_{yz}=\frac{1}{\sqrt{2}}\left[(\lambda_{y}^{2}+\lambda_{z}^{2})+\sqrt{(\lambda_{y}^{2}+\lambda_{z}^{2})^{2}-4(1-\frac{y_{s}^{2}}{i_{0}^{2}})\lambda_{y}^{2}\lambda_{z}^{2}}\right]^{\frac{1}{2}} \tag{7.2.2-4} $$
式中: $ y_{s} $ ——截面形心至剪心的距离(mm);
$ i_{0} $ ——截面对剪心的极回转半径,单轴对称截面 $ i_{0}^{2}=y_{s}^{2}+i_{x}^{2}+i_{y}^{2} $ (mm);
$ \lambda_{z} $ ——扭转屈曲换算长细比,由式(7.2.2-3)确定。
2)等边单角钢轴心受压构件当绕两主轴弯曲的计算长度相等时,可不计算弯扭屈曲。塔架单角钢压杆应符合本标准第7.6节的相关规定。
3) 双角钢组合 T 形截面构件绕对称轴的换算长细比 $ \lambda_{yz} $ 可按下列简化公式确定:
等边双角钢(图 7.2.2-1(a)):
当 $ \lambda_{y}\geq\lambda_{z} $ 时:
$$ \lambda_{yz}=\lambda_{y}\left[1+0.16(\frac{\lambda_{z}}{\lambda_{y}})^{2}\right] \tag{7.2.2-5} $$
当 $ \lambda_{y}<\lambda_{z} $ 时:
$$ \lambda_{yz}=\lambda_{z}\Bigg[1+0.16(\frac{\lambda_{y}}{\lambda_{z}})^{2}\Bigg] \tag{7.2.2-6} $$
$$ \lambda_{z}=3.9\frac{b}{t} \tag{7.2.2-7} $$
长肢相并的不等边双角钢(图 7.2.2-1(b)):
当 $ \lambda_{y}\geq\lambda_{z} $ 时:
$$ \lambda_{\mathrm{yz}}=\lambda_{\mathrm{y}}\left[1+0.25(\frac{\lambda_{\mathrm{z}}}{\lambda_{\mathrm{y}}})^{2}\right] \tag{7.2.2-8} $$
当 $ \lambda_{y}<\lambda_{z} $ 时:
$$ \lambda_{yz}=\lambda_{z}\left[1+0.25(\frac{\lambda_{y}}{\lambda_{z}})^{2}\right] \tag{7.2.2-9} $$
$$ \lambda_{z}=5.1\frac{b_{2}}{t} \tag{7.2.2-10} $$
短肢相并的不等边双角钢(图 7.2.2-1(c)):
当 $ \lambda_{y}\geq\lambda_{z} $ 时:
$$ \lambda_{\mathrm{yz}}=\lambda_{\mathrm{y}}\left[1+0.06(\frac{\lambda_{\mathrm{z}}}{\lambda_{\mathrm{y}}})^{2}\right] \tag{7.2.2-11} $$
当 $ \lambda_{y}<\lambda_{z} $ 时:
$$ \lambda_{yz}=\lambda_{z}\left[1+0.06(\frac{\lambda_{y}}{\lambda_{z}})^{2}\right] \tag{7.2.2-12} $$
$$ \lambda_{z}=3.7\frac{b_{1}}{t} \tag{7.2.2-13} $$
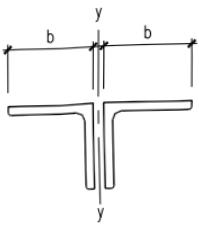
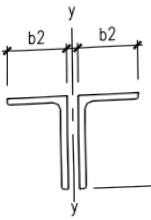
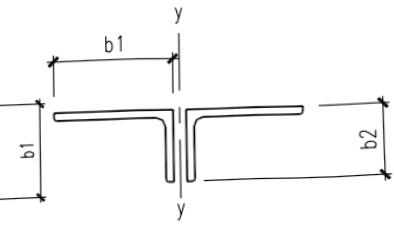
b—等边角钢肢宽度; $ b_{1} $ —不等边角钢长肢宽度; $ b_{2} $ —不等边角钢短肢宽度
3 截面无对称轴且剪心和形心不重合的构件,应采用下列换算长细比:
$$ \lambda_{xyz}=\pi\sqrt{\frac{EA}{N_{xyz}}} \tag{7.2.2-14} $$
$$ (N_{\mathrm{x}}-N_{\mathrm{xyz}})(N_{\mathrm{y}}-N_{\mathrm{xyz}})(N_{\mathrm{z}}-N_{\mathrm{xyz}})-N_{\mathrm{xyz}}^{2}(N_{\mathrm{x}}-N_{\mathrm{xyz}})(\frac{y_{\mathrm{s}}}{i_{0}})^{2}-N_{\mathrm{xyz}}^{2}(N_{\mathrm{y}}-N_{\mathrm{xyz}})(\frac{x_{\mathrm{s}}}{i_{0}})^{2}=0 \tag{7.2.2-15} $$
$$ i_{0}^{2}=i_{x}^{2}+i_{y}^{2}+x_{s}^{2}+y_{s}^{2} \tag{7.2.2-16} $$
$$ N_{x}=\frac{\pi^{2}EA}{\lambda_{x}^{2}} \tag{7.2.2-17} $$
$$ N_{y}=\frac{\pi^{2}EA}{\lambda_{y}^{2}} \tag{7.2.2-18} $$
$$ N_{{z}}=\frac{1}{iEI_{}^{2}}(\frac{\pi^{2\omega}}{l{\omega}^{2}}+GI $$}}) \tag{7.2.2-19
式中: $ N_{xyz} $ ——弹性完善杆的弯扭屈曲临界力,由式(7.2.2-15)确定(N):
$ x_{s} $ 、 $ y_{s} $ ——截面剪心的坐标(mm);
$ i_{0} $ ——截面对剪心的极回转半径(mm);
$ N_{x} $ 、 $ N_{y} $ 、 $ N_{z} $ ——分别为绕x轴和y轴的弯曲屈曲临界力和扭转屈曲临界力(N):
E、G——分别为钢材弹性模量和剪变模量(N/mm $ ^{2} $ )。
4 不等边角钢轴心受压构件的换算长细比可按下列简化公式确定(图 7.2.2-2):
当 $ \lambda_{v}\geq\lambda_{z} $ 时:
$$ \lambda_{\mathrm{xyz}}=\lambda_{\mathrm{v}}\left[1+0.25\left(\frac{\lambda_{\mathrm{z}}}{\lambda_{\mathrm{v}}}\right)^{2}\right] \tag{7.2.2-20} $$
当 $ \lambda_{v}<\lambda_{z} $ 时:
$$ \lambda_{\mathrm{x y z}}=\lambda_{\mathrm{z}}\left[1+0.25\left(\frac{\lambda_{\mathrm{v}}}{\lambda_{\mathrm{z}}}\right)^{2}\right] \tag{7.2.2-21} $$
$$ \lambda_{z}=4.21\frac{b_{1}}{t} \tag{7.2.2-22} $$
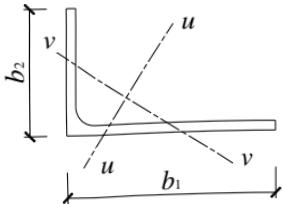
注:v 轴为角钢的弱轴, $ b_{1} $ 为角钢长肢宽度
7.2.3¶
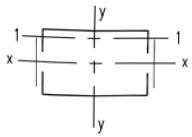
格式轴心受压构件的稳定性应按本标准式(7.2.1)计算,对实轴的长细比应按本标准式(7.2.2-1)或式(7.2.2-2)计算,对虚轴(图7.2.3(a))的x轴和图7.2.3(b)、图7.2.3(c)的x轴和y轴应取换算长细比。换算长细比应按下列公式计算:
1 双肢组合构件(图 7.2.3(a)):
当缀件为缀板时:
$$ \lambda_{0x}=\sqrt{\lambda_{x}^{2}+\lambda_{1}^{2}} \tag{7.2.3-1} $$
当缀件为缀条时:
$$ \lambda_{0x}=\sqrt{\lambda_{x}^{2}+27\frac{A}{A_{1x}}} \tag{7.2.3-2} $$
式中: $ \lambda_{x} $ ——整个构件对 x 轴的长细比;
$ \lambda_{1} $ ——分肢对最小刚度轴1-1的长细比,其计算长度取为:焊接时,为相邻两缀板的净距离;螺栓连接时,为相邻两缀板边缘螺栓的距离;
$ A_{1x} $ ——构件截面中垂直于 x 轴的各斜缀条毛截面面积之和(mm²)。
2 四肢组合构件(图 7.2.3(b)):
当缀件为缀板时:
$$ \lambda_{0x}=\sqrt{\lambda_{x}^{2}+\lambda_{1}^{2}} \tag{7.2.3-3} $$
$$ \lambda_{0y}=\sqrt{\lambda_{y}^{2}+\lambda_{1}^{2}} \tag{7.2.3-4} $$
当缀件为缀条时:
$$ \lambda_{0x}=\sqrt{\lambda_{x}^{2}+40\frac{A}{A_{1x}}} \tag{7.2.3-5} $$
$$ \lambda_{0y}=\sqrt{\lambda_{y}^{2}+40\frac{A}{A_{1y}}} \tag{7.2.3-6} $$
式中: $ \lambda_{y} $ ——整个构件对 y 轴的长细比;
$ A_{1y} $ ——构件截面中垂直于 y 轴的各斜缀条毛截面面积之和(mm²)。
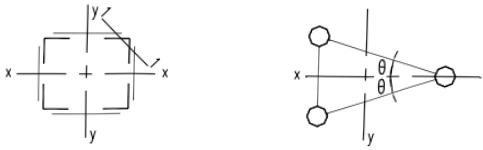
3 缀件为缀条的三肢组合构件(图 7.2.3(c)):
$$ \lambda_{0x}=\sqrt{\lambda_{x}^{2}+\frac{42A}{A_{1}(1.5-\cos^{2}\theta)}} \tag{7.2.3-7} $$
$$ \lambda_{0y}=\sqrt{\lambda_{y}^{2}+\frac{42A}{A_{1}\cos^{2}\theta}} \tag{7.2.3-8} $$
式中: $ A_{1} $ ——构件截面中各斜缀条毛截面面积之和(mm $ ^{2} $ );
$ \theta $ ——构件截面内缀条所在平面与x轴的夹角。
7.2.4¶
缀件面宽度较大的格构式柱宜采用缀条柱,斜缀条与构件轴线间的夹角应为 $ 40^{\circ} $ ~ $ 70^{\circ} $ 。缀条柱的分肢长细比 $ \lambda_{1} $ 不应大于构件两方向长细比较大值 $ \lambda_{max} $ 的0.7倍,对虚轴取换算长细比。格构式柱和大型实腹式柱,在受有较大水平力处和运送单元的端部应设置横隔,横隔的间距不宜大于柱截面长边尺寸的9倍且不宜大于8m。
7.2.5¶
缀板柱的分肢长细比 $ \lambda_{1} $ 不应大于 $ 40\varepsilon_{k} $ ,并不应大于 $ \lambda_{max} $ 的 0.5 倍,当 $ \lambda_{max} < 50 $ 时,取 $ \lambda_{max} = 50 $ 。缀板柱中同一截面处缀板或型钢横杆的线刚度之和不得小于柱较大分肢线刚度的 6 倍。
7.2.6¶
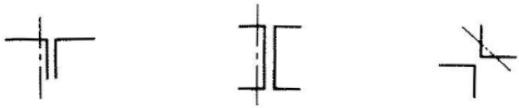
用填板连接而成的双角钢或双槽钢构件,采用普通螺栓连接时应按格构式构件进行计算;除此之外,可按实腹式构件进行计算,但受压构件填板间的距离不应超过40i,受拉构件填板间的距离不应超过80i。i为单肢截面回转半径,应按下列规定采用:
1 当为图 7.2.6(a)、(b)所示的双角钢或双槽钢截面时,取一个角钢或一个槽钢对与填板平行的形心轴的回转半径;
2 当为图 7.2.6(c)所示的十字形截面时,取一个角钢的最小回转半径。受压构件的两个侧向支承点之间的填板数不应少于 2 个。
7.2.7¶
轴心受压构件剪力 V 值可认为沿构件全长不变,格构式轴心受压构件的剪力 V 应由承受该剪力的缀材面(包括用整体板连接的面)分担,其值应按下式计算:
$$ V=\frac{Af}{85\varepsilon_{k}} \tag{7.2.7-1} $$
7.2.8¶
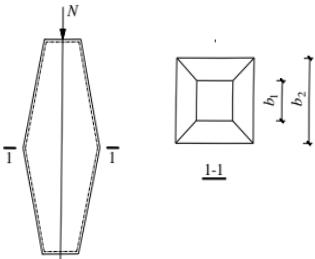
两端铰支的梭形圆管或方管状截面轴心受压构件(图 7.2.8)的稳定性应按本标准式(7.2.1)计算。其中 A 取端截面的截面面积 $ A_{1} $ ,稳定系数 $ \varphi $ 应根据按下列公式计算的换算长细比 $ \lambda_{e} $ 确定:
$$ \lambda_{\mathrm{e}}=\frac{l_{0}\;/\;i_{1}}{\left(1+\gamma\right)^{3/4}} \tag{7.2.8-1} $$
$$ l_{0}=\frac{l}{2}\Big[1+\left(1+0.853\gamma\right)^{-1}\Big] \tag{7.2.8-2} $$
$$ \gamma=(D_{2}-D_{1})/D_{1} 或 (b_{2}-b_{1})/b_{1} \tag{7.2.8-3} $$
式中: $ l_{0} $ ——构件计算长度(mm);
$ i_{1} $ ——端截面回转半径(mm);
γ——构件楔率;
$ D_{2} $ 、 $ b_{2} $ ——分别为跨中截面圆管外径和方管边长(mm);
$ D_{1} $ 、 $ b_{1} $ ——分别为端截面圆管外径和方管边长(mm)。
7.2.9¶
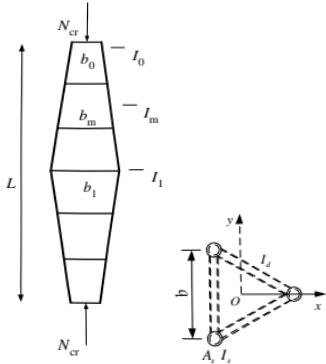
钢管梭形格构柱的跨中截面应设置横隔。横隔可采用水平放置的钢板且与周边缀管焊接,也可采用水平放置的钢管并使跨中截面成为稳定截面。两端铰支的三肢钢管梭形格构柱应按本标准式(7.2.1)计算整体稳定。稳定系数 $ \varphi $ 应根据下列公式计算的换算长细比 $ \lambda_{0} $ 确定:
$$ \lambda_{0}=\pi\sqrt{\frac{3A_{s}E}{N_{cr}}} \tag{7.2.9-1} $$
$$ N_{\mathrm{cr}}=\min\left(N_{\mathrm{cr,s}},N_{\mathrm{cr,a}}\right) \tag{7.2.9-2} $$
$ N_{cr,s} $ 应按下列公式计算:
$$ N_{\mathrm{cr},s}=N_{\mathrm{cr0},s}\ /\ (1+\frac{N_{\mathrm{cr0},s}}{K_{\mathrm{v},s}}) \tag{7.2.9-3} $$
$$ N_{\mathrm{cr0,s}}=\frac{\pi^{2}EI_{0}}{L^{2}}(1+0.72\eta_{1}+0.28\eta_{2}) \tag{7.2.9-4} $$
$ N_{cr,a} $ 应按下列公式计算:
$$ N_{\mathrm{cr,a}}=N_{\mathrm{cr0,a}}/\left(1+\frac{N_{\mathrm{cr0,a}}}{K_{\mathrm{v,a}}}\right) \tag{7.2.9-5} $$
$$ N_{\mathrm{cr0,a}}=\frac{4\pi^{2}EI_{0}}{L^{2}}(1+0.48\eta_{1}+0.12\eta_{2}) \tag{7.2.9-6} $$
$ \eta_{1} $ 、 $ \eta_{2} $ 应按下列公式计算:
$$ \eta_{1}=(4I_{\mathrm{m}}-I_{1}-3I_{0})/I_{0} \tag{7.2.9-7} $$
$$ \eta_{2}=2(I_{0}+I_{1}-2I_{\mathrm{m}})/I_{0} \tag{7.2.9-8} $$
$$ I_{0}=3I_{\mathrm{s}}+0.5b_{0}^{2}A_{\mathrm{s}} \tag{7.2.9-9} $$
$$ I_{\mathrm{m}}=3I_{\mathrm{s}}+0.5b_{\mathrm{m}}^{2}A_{\mathrm{s}} \tag{7.2.9-10} $$
$$ I_{1}=3I_{\mathrm{s}}+0.5b_{1}^{2}A_{\mathrm{s}} \tag{7.2.9-11} $$
$$ K_{\mathrm{v,s}}=1\Bigg/\Bigg(\frac{l_{\mathrm{s0}}b_{0}}{18EI_{\mathrm{d}}}+\frac{5l_{\mathrm{s0}}^{2}}{144EI_{\mathrm{s}}}\Bigg) \tag{7.2.9-12} $$
$$ K_{\mathrm{v,a}}=1\Bigg/\Bigg(\frac{l_{\mathrm{s0}}b_{\mathrm{m}}}{18EI_{\mathrm{d}}}+\frac{5l_{\mathrm{s0}}^{2}}{144EI_{\mathrm{s}}}\Bigg) \tag{7.2.9-13} $$
式中: $ A_{s} $ ——单根分肢的截面面积(mm $ ^{2} $ );
$ N_{cr} $ 、 $ N_{cr,s} $ 、 $ N_{cr,a} $ ——分别为特征值屈曲荷载、对称屈曲模态与反对称屈曲模态对应的特征值
屈曲荷载(N);
$ I_{0} $ 、 $ I_{m} $ 、 $ I_{1} $ ——分别为钢管梭形格构柱柱端、1/4跨处以及跨中截面对应的惯性矩(图7.2.9)
$$ (mm^{4}); \tag{7.2.9-14} $$
$ K_{v,s} $ 、 $ K_{v,a} $ ——分别为对称屈曲与反对称屈曲对应的截面抗剪刚度(N);
$ \eta_{1} $ 、 $ \eta_{2} $ ——与截面惯性矩有关的计算系数;
$ b_{0} $ 、 $ b_{m} $ 、 $ b_{1} $ ——分别为梭形柱柱端、1/4跨处和跨中截面的边长(mm);
$ l_{s0} $ ——梭形柱节间高度(mm);
$ I_{d} $ 、 $ I_{s} $ ——横缀杆和弦杆的惯性矩(mm $ ^{4} $ );
$ A_{s} $ ——单个分肢的截面面积(mm $ ^{2} $ );
E——材料的弹性模量(N/mm $ ^{2} $ )。
7.3 实腹式轴心受压构件的局部稳定和屈曲后强度¶
7.3.1¶
实腹轴心受压构件要求不出现局部失稳者,其板件宽厚比应符合下列规定:
1 H形截面腹板
$$ h_{0}/t_{w}\leq\left(25+0.5\lambda\right)\varepsilon_{k} \tag{7.3.1-1} $$
式中: $ \lambda $ ——构件的较大长细比;当 $ \lambda<30 $ 时,取为30;当 $ \lambda>100 $ 时,取为100;
$ h_{0} $ 、 $ t_{w} $ ——分别为腹板计算高度和厚度,按本标准表3.5.1注2取值。
2 H形截面翼缘
$$ b/t_{\mathrm{f}}\leq\left(10+0.1\lambda\right)\varepsilon_{\mathrm{k}} \tag{7.3.1-2} $$
式中:b、 $ t_{f} $ ——分别为翼缘板自由外伸宽度和厚度,按本标准表3.5.1注2取值。
3 箱形截面壁板
$$ b/t\leq40\varepsilon_{k} \tag{7.3.1-3} $$
式中:b——壁板的净宽度。当箱形截面设有纵向加劲肋时,为壁板与加劲肋之间的净宽度。
4 T形截面翼缘宽厚比限值应按式 $ (7.3.1-2) $ 确定。
T形截面腹板宽厚比限值为:
热轧剖分 T 形钢
$$ h_{0}/t_{w}\leq\left(15+0.2\lambda\right)\varepsilon_{k} \tag{7.3.1-4} $$
焊接 T 形钢
$$ h_{0}/t_{w}\leq\left(13+0.17\lambda\right)\varepsilon_{k} \tag{7.3.1-5} $$
对焊接构件 $ h_{0} $ 取腹板高度 $ h_{w} $ ;对热轧构件, $ h_{0} $ 取腹板平直段长度,简要计算时可取 $ h_{0}=h_{w}-t_{f} $ ,但不小于 $ h_{w}-20~mm $ 。
5 等边角钢轴心受压构件的肢件宽厚比限值为:
当 $ \lambda\leq80\varepsilon_{k} $ 时:
$$ w/t\leq15\varepsilon_{k} \tag{7.3.1-6} $$
$$ \lambda>80\varepsilon_{\mathrm{k}} \tag{7.3.1-7} $$
$$ w/t\leq5\varepsilon_{\mathrm{k}}+0.125\lambda \tag{7.3.1-8} $$
式中:w、t——分别为角钢的平板宽度和厚度,简要计算时w可取为b-2t,b为角钢宽度;
$ \lambda $ ——按角钢绕非对称主轴回转半径计算的长细比。
6 圆管压杆的外径与壁厚之比不应超过 $ 100\varepsilon_{k}^{2} $
7.3.2¶
当轴心受压构件的压力小于稳定承载力 $ \varphi A f $ 时,可将其板件宽厚比限值由本标准第
7.3.1¶
条相关公式算得后乘以放大系数 $ \alpha = \sqrt{\varphi Af / N} $ 确定。
7.3.3¶
板件宽厚比超过本标准第 7.3.1 条规定的限值时,可采用纵向加劲肋加强;当可考虑屈曲后强度时,轴心受压杆件的强度和稳定性可按下列公式计算:
强度计算
$$ \frac{N}{A_{ne}}\leq f \tag{7.3.3-1} $$
稳定性计算
$$ \frac{N}{\varphi A_{\mathrm{e}}f}\leq1.0 \tag{7.3.3-2} $$
$$ A_{\mathrm{ne}}=\sum\rho_{i}A_{\mathrm{ni}} \tag{7.3.3-3} $$
$$ A_{\mathrm{e}}{=}\sum\rho_{i}A_{i} \tag{7.3.3-4} $$
式中: $ A_{ne} $ 、 $ A_{e} $ ——分别为有效净截面面积和有效毛截面面积;
$ A_{ni} $ 、 $ A_{i} $ ——分别为各板件净截面面积和毛截面面积;
$ \varphi $ ——稳定系数,可按毛截面计算;
$ \rho_{i} $ ——各板件有效截面系数,可按本标准第7.3.4条的规定计算。
7.3.4¶
H形、工字形、箱形和单角钢截面轴心受压构件的有效截面系数 $ \rho $ 可按下列规定计算:
1 箱形截面的壁板、H形或工字形的腹板:
当 $ \lambda\leq40\varepsilon_{k} $ 时:
$$ \rho=1.0 \tag{7.3.4-1} $$
当 $ \lambda>52\varepsilon_{k} $ 时:
$$ \rho\geq\big(29\varepsilon_{\mathrm{k}}+0.25\lambda\big)t/b \tag{7.3.4-2} $$
当 $ b/t>42\varepsilon_{k} $ 时:
$$ \rho=\frac{1}{\lambda_{n,p}}\left(1-\frac{0.19}{\lambda_{n,p}}\right) \tag{7.3.4-3} $$
$$ \lambda_{n,p}=\frac{b/t}{56.2\varepsilon_{k}} \tag{7.3.4-4} $$
式中:b、t——分别为壁板或腹板的净宽度和厚度。
2 单角钢:
$$ \lambda>80\varepsilon_{k} \tag{7.3.4-5} $$
$$ \rho\geq\big(5\varepsilon_{\mathrm{k}}+0.13\lambda\big)t/w \tag{7.3.4-6} $$
当 $ w/t>15\varepsilon_{k} $ 时:
$$ \rho=\frac{1}{\lambda_{\mathrm{n,p}}}\left(1-\frac{0.1}{\lambda_{\mathrm{n,p}}}\right) \tag{7.3.4-7} $$
$$ \lambda_{{n,p}}=\frac{w/t}{16.8\varepsilon $$}}} \tag{7.3.4-8
7.3.5¶
H形、工字形和箱形截面轴心受压构件的腹板,当用纵向加劲肋加强以满足宽厚比限值时,加劲肋宜在腹板两侧成对配置,其一侧外伸宽度不应小于 $ 10t_{w} $ ,厚度不应小于 $ 0.75t_{w} $ 。
7.4 轴心受力构件的计算长度和容许长细比¶
7.4.1¶
确定桁架弦杆和单系腹杆的长细比时,其计算长度 $ l_{0} $ 应按表7.4.1-1采用;采用相贯焊接连接的钢管桁架,其构件计算长度 $ l_{0} $ 可按表7.4.1-2取值;除钢管结构外,无节点板的腹杆计算长度在任意平面内均应取其等于几何长度。桁架再分式腹杆体系的受压主斜杆及K型腹杆体系的竖杆等,在桁架平面内的计算长度则取节点中心间距离。
| 弯曲方向 | 弦杆 | 腹杆 | |
| 支座斜杆和支座竖杆 | 其他腹杆 | ||
| 桁架平面内 | l | l | 0.8l |
| 桁架平面外 | l1 | l | l |
| 斜平面 | — | l | 0.9l |
注:1 l 为构件的几何长度(节点中心间距离), $ l_{1} $ 为桁架弦杆侧向支承点之间的距离。
2 斜平面系指与桁架平面斜交的平面,适用于构件截面两主轴均不在桁架平面内的单角钢腹杆和双角钢十字形截面腹杆。
| 桁架类别 | 弯曲方向 | 弦杆 | 腹杆 | |
| 支座斜杆和支座竖杆 | 其他腹杆 | |||
| 平面桁架 | 平面内 | 0.9l | l | 0.8l |
| 平面外 | l1 | l | l | |
| 立体桁架 | 0.9l | l | 0.8l | |
注: $ 1l_{1} $ 为平面外无支撑长度,l 为杆件的节间长度。
2 对端部缩头或压扁的圆管腹杆,其计算长度取 l 。
3 对于立体桁架,弦杆平面外的计算长度取 0.9l,同时尚应以 $ 0.9l_{1} $ 按格构式压杆验算其稳定性。
7.4.2¶
确定在交叉点相互连接的桁架交叉腹杆的长细比时,在桁架平面内的计算长度应取节点中心到交叉点的距离;在桁架平面外的计算长度,当两交叉杆长度相等且在中点相交时,应按下列规定采用:
1 压杆。
1)相交另一杆受压,两杆截面相同并在交叉点均不中断,则:
$$ l_{0}=l\sqrt{\frac{1}{2}(1+\frac{N_{0}}{N})} \tag{7.4.2-1} $$
2)相交另一杆受压,此另一杆在交叉点中断但以节点板搭接,则:
$$ l_{0}=l\sqrt{1+\frac{\pi^{2}}{12}\cdot\frac{N_{0}}{N}} \tag{7.4.2-2} $$
3)相交另一杆受拉,两杆截面相同并在交叉点均不中断,则:
$$ l_{0}=l\sqrt{\frac{1}{2}(1-\frac{3}{4}\cdot\frac{N_{0}}{N})}\geq0.5l \tag{7.4.2-3} $$
4)相交另一杆受拉,此拉杆在交叉点中断但以节点板搭接,则:
$$ l_{0}=l\sqrt{1-\frac{3}{4}\cdot\frac{N_{0}}{N}}\geq0.5l \tag{7.4.2-4} $$
5) 当拉杆连续而压杆在交叉点中断但以节点板搭接,若 $ N_{0} \geq N $ 或拉杆在桁架平面外的弯曲刚度 $ EI_{y} \geq \frac{3N_{0}l^{2}}{4\pi^{2}}\left(\frac{N}{N_{0}}-1\right) $ 时,取 $ l_{0} = 0.5l $ 。
式中:l ——桁架节点中心间距离(交叉点不作为节点考虑)(mm);
N、 $ N_{0} $ ——所计算杆的内力及相交另一杆的内力,均为绝对值。两杆均受压时,取 $ N_{0}\leq N $ ,两杆截面应相同(N)。
2 拉杆,应取 $ l_{0}=l $ 。当确定交叉腹杆中单角钢杆件斜平面内的长细比时,计算长度应取节点中心至交叉点的距离。当交叉腹杆为单边连接的单角钢时,应按本标准第7.6.2条的规定确定杆件等效长细比。
7.4.3¶
当桁架弦杆侧向支承点之间的距离为节间长度的2倍(图7.4.3)且两节间的弦杆轴心压力不相同时,则该弦杆在桁架平面外的计算长度应按下式确定(但不应小于 $ 0.5l_{1} $ ):
$$ l_{0}=l_{1}\Bigg(0.75+0.25\frac{N_{2}}{N_{1}}\Bigg) \tag{7.4.3-1} $$
式中: $ N_{1} $ ——较大的压力,计算时取正值;
$ N_{2} $ ——较小的压力或拉力,计算时压力取正值,拉力取负值。
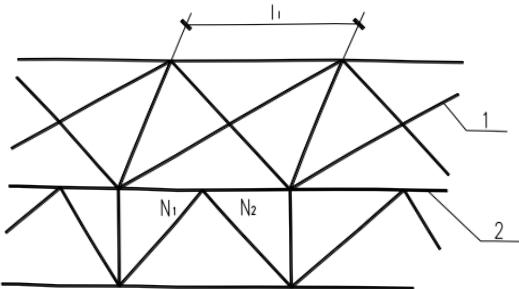
1—支撑;2—桁架
7.4.4¶
塔架的单角钢主杆,应按所在两个侧面的节点分布情况,采用下列长细比确定稳定系数 $ \varphi $ :
1 当两个侧面腹杆体系的节点全部重合时(图 7.4.(4a)):
$$ \lambda=l/i_{\mathrm{y}} \tag{7.4.4-1} $$
2 当两个侧面腹杆体系的节点部分重合时(图 7.4.4(b)):
$$ \lambda=1.1l/i_{\mathrm{u}} \tag{7.4.4-2} $$
3 当两个侧面腹杆体系的节点全部都不重合时(图 7.4.4(c)):
$$ \lambda=1.2l/i_{\mathrm{u}} \tag{7.4.4-3} $$
式中: $ i_{v} $ ——截面绕非对称主轴的回转半径;
l, $ i_{u} $ ——分别为较大的节间长度和绕平行轴的回转半径。
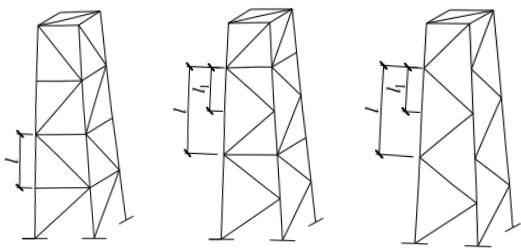
(a) 两个侧面腹杆体系 (b) 两个侧面腹杆体系 (c) 两个侧面腹杆体系的节点全部重合的节点部分重合的节点全部都不重合
4 当角钢宽厚比符合本标准第 7.3.4 条第 2 款要求时,应按该款规定确定系数 $ \varphi $ ,并按本标准第 7.3.3 条的规定计算主杆的承载力。
7.4.5¶
塔架单角钢人字形或 V 形主斜杆,当辅助杆多于两道时,宜连接两相邻侧面的主斜杆以减小其计算长度。当连接有不多于两道辅助杆时,其长细比宜乘以 1.1 的放大系数。
7.4.6¶
验算容许长细比时,可不考虑扭转效应,计算单角钢受压构件的长细比时,应采用角钢的最小回转半径,但计算在交叉点相互连接的交叉杆件平面外的长细比时,可采用与角钢肢边平行轴的回转半径。轴心受压构件的容许长细比宜符合下列规定:
1 跨度等于或大于 $ 60 \, m $ 的桁架,其受压弦杆、端压杆和直接承受动力荷载的受压腹杆的长细比不宜大于 120。
2 轴心受压构件的长细比不宜超过表 7.4.6 规定的容许值,但当杆件内力设计值不大于承载能力的 50% 时,容许长细比值可取 200。
| 构件名称 | 容许长细比 |
| 轴心受压柱、桁架和天窗架中的压杆 | 150 |
| 柱的缀条、吊车梁或吊车桁架以下的柱间支撑 | 150 |
| 支撑 | 200 |
| 用以减小受压构件计算长度的杆件 | 200 |
7.4.7¶
验算容许长细比时,在直接或间接承受动力荷载的结构中,计算单角钢受拉构件的长细比时,应采用角钢的最小回转半径,但计算在交叉点相互连接的交叉杆件平面外的长细比时,可采用与角钢肢边平行轴的回转半径。受拉构件的容许长细比宜符合下列规定:
1 除对腹杆提供平面外支点的弦杆外,承受静力荷载的结构受拉构件,可仅计算竖向平面内的长细比。
2 中、重级工作制吊车桁架下弦杆的长细比不宜超过 200。
3 在设有夹钳或刚性料耙等硬钩起重机的厂房中,支撑的长细比不宜超过 300。
4 受拉构件在永久荷载与风荷载组合作用下受压时,其长细比不宜超过 250。
5 跨度等于或大于 60m 的桁架,其受拉弦杆和腹杆的长细比,承受静力荷载或间接承受动力荷载时不宜超过 300,直接承受动力荷载时,不宜超过 250。
6 受拉构件的长细比不宜超过表 7.4.7 规定的容许值。柱间支撑按拉杆设计时,竖向荷
载作用下柱子的轴力应按无支撑时考虑。
| 构件名称 | 承受静力荷载或间接受动力荷载的结构 | 直接承受动力荷载的结构 | ||
| 一般建筑结构 | 对腹杆提供平面外支点的弦杆 | 有重级工作制起重机的厂房 | ||
| 桁架的构件 | 350 | 250 | 250 | 250 |
| 吊车梁或吊车桁架以下柱间支撑 | 300 | — | 200 | |
| 除张紧的圆钢外的其他拉杆、支撑、系杆等 | 400 | — | 350 | — |
7.4.8¶
上端与梁或桁架铰接且不能侧向移动的轴心受压柱,计算长度系数应根据柱脚构造情况采用,对铰轴柱脚应取1.0,对底板厚度不小于柱翼缘厚度2倍的平板支座柱脚可取为0.8。由侧向支撑分为多段的柱,当各段长度相差10%以上时,宜根据相关屈曲的原则确定柱在支撑平面内的计算长度。
7.5 轴心受压构件的支撑¶
7.5.1¶
用作减小轴心受压构件自由长度的支撑,应能承受沿被撑构件屈曲方向的支撑力,其值应按下列方法计算:
1 长度为 l 的单根柱设置一道支撑时,支撑力 $ F_{b1} $ 应按下列公式计算:
当支撑杆位于柱高度中央时:
$$ F_{\mathrm{b l}}=N/60 \tag{7.5.1-1} $$
当支撑杆位于距柱端 $ \alpha l $ 处时( $ 0 < \alpha < 1 $ ):
$$ F_{\mathrm{b l}}=\frac{N}{240\alpha\left(1-\alpha\right)} \tag{7.5.1-2} $$
2 长度为 l 的单根柱设置 m 道等间距及间距不等但与平均间距相比相差不超过 20% 的支撑时,各支承点的支撑力 $ F_{bm} $ 应按下式计算:
$$ F_{\mathrm{bm}}=\frac{N}{42\sqrt{m+1}} \tag{7.5.1-3} $$
3 被撑构件为多根柱组成的柱列,在柱高度中央附近设置一道支撑时,支撑力应按下式计算:
$$ F_{\mathbf{b}n}=\frac{\sum N_{i}}{60}\Bigg(0.6+\frac{0.4}{n}\Bigg) \tag{7.5.1-4} $$
式中:N —— 被撑构件的最大轴心压力(N);
n——柱列中被撑柱的根数;
$ \sum N_{i} $ ——被撑柱同时存在的轴心压力设计值之和(N)。
4 当支撑同时承担结构上其他作用的效应时,应按实际可能发生的情况与支撑力组合。
5 支撑的构造应使被撑构件在撑点处既不能平移,又不能扭转。
7.5.2¶
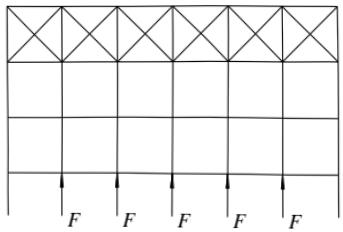
桁架受压弦杆的横向支撑系统中系杆和支承斜杆应能承受下式给出的节点支撑力(图7.5.2):
$$ F=\frac{\sum N}{42\sqrt{m+1}}(0.6+\frac{0.4}{n}) \tag{7.5.2-1} $$
式中: $ \sum N $ ——被撑各桁架受压弦杆最大压力之和(N);
m——纵向系杆道数(支撑系统节间数减去1);
n——支撑系统所撑桁架数。
7.5.3¶
塔架主杆与主斜杆之间的辅助杆(图 7.5.3)应能承受下列公式给出的节点支撑力:当节间数不超过 4 时:
$$ F=N/80 \tag{7.5.3-1} $$
当节间数大于4时:
$$ F=N/100 \tag{7.5.3-2} $$
式中:N——主杆压力设计值(N)。
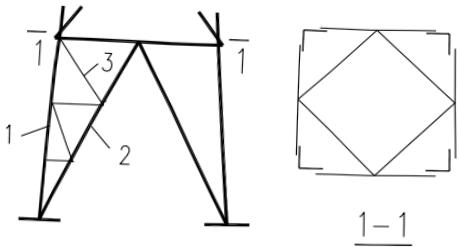
1—主杆;2—主斜杆;3—辅助杆
7.6 单边连接的单角钢¶
7.6.1¶
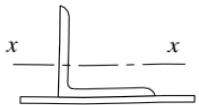
桁架的单角钢腹杆,当以一个肢连接于节点板时(图 7.6.1),除弦杆亦为单角钢,并位于节点板同侧者外,应符合下列规定:
1 轴心受力构件的截面强度应按本标准式(7.1.1-1)和(7.1.1-2)计算,但强度设计值应乘以折减系数0.85。
2 受压构件的稳定性应按下列公式计算:
$$ \frac{N}{\eta\varphi A f}\leq1.0 \tag{7.6.1-1} $$
等边角钢
$$ \eta=0.6+0.0015\lambda \tag{7.6.1-2} $$
短边相连的不等边角钢
$$ \eta=0.5+0.0025\lambda \tag{7.6.1-3} $$
长边相连的不等边角钢
$$ \eta=0.7 \tag{7.6.1-4} $$
式中: $ \lambda $ ——长细比,对中间无联系的单角钢压杆,应按最小回转半径计算,当 $ \lambda<20 $ 时,取 $ \lambda=20 $ ;
$ \eta $ ——折减系数,当计算值大于1.0时取为1.0。
3 当受压斜杆用节点板和桁架弦杆相连接时,节点板厚度不宜小于斜杆肢宽的 1/8。
7.6.2¶
塔架单边连接单角钢交叉斜杆中的压杆,当两杆截面相同并在交叉点均不中断,计算其平面外的稳定性时,稳定系数 $ \varphi $ 应由下列等效长细比查本标准附录 D 表格确定:
$$ \lambda_{0}=\alpha_{e}\mu_{u}\lambda_{e}\geq\frac{l_{1}}{l}\lambda_{x} \tag{7.6.2-1} $$
当 $ 20 \leq \lambda_{u} \leq 80 $ 时:
$$ \lambda_{\mathrm{e}}=80+0.65\lambda_{\mathrm{u}} \tag{7.6.2-2} $$
当 $ 80<\lambda_{u}\leq160 $ 时:
$$ \lambda_{\mathrm{e}}=52+\lambda_{\mathrm{u}} \tag{7.6.2-3} $$
当 $ \lambda_{u}>160 $ 时:
$$ \lambda_{\mathrm{e}}=20+1.2\lambda_{\mathrm{u}} \tag{7.6.2-4} $$
$$ \lambda_{{u}}=\frac{l}{i{{u}}}\cdot\frac{1}{\varepsilon $$}}} \tag{7.6.2-5
$$ \mu_{\mathrm{u}}=l_{0}/l \tag{7.6.2-6} $$
式中: $ \alpha_{e} $ ——系数,应按表7.6.2的规定取值;
$ \mu_{u} $ ——计算长度系数;
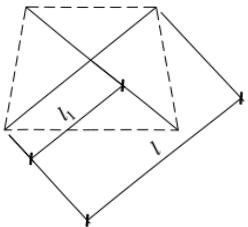
$ l_{1} $ ——交叉点至节点间的较大距离(图7.6.2)(mm);
$ \lambda_{e} $ ——换算长细比;
$ l_{0} $ ——计算长度,当相交另一杆受压,应按本标准式(7.4.2-1)计算;当相交另一杆受拉,应按本标准式(7.4.2-3)计算(mm)。
| 主杆截面 | 另杆受拉 | 另杆受压 | 另杆不受力 |
| 单角钢 | 0.75 | 0.90 | 0.75 |
| 双轴对称截面 | 0.90 | 0.75 | 0.90 |
$$ \rho_{e}^{}=1.3-\frac{0.3w}{14t_{3}} \tag{7.6.2-7} $$
(7.6.1-1) 确定的稳定承载力应乘以按下式计算的折减系数 $ \rho_{s} $ :
7.6.3¶
单边连接的单角钢压杆,当肢件宽厚比w/t大于14g时,由本标准式(7.2.1)和式